A table of cumulative frequencies

Part 1: Point updates

Today’s problem comes from a school.

Many students have taken their mid-year exams recently, and the results are out! Each student has been given a mark between 1 and 100. So the principal has approached you with a problem to solve. Given a range of marks, the principal wants to know how many students in total scored marks within that range.

That’s exactly what this article is about. Though the title sounds scary, it’s actually quite simple. But the principal isn’t going to wait all day, so you’d better get your problem-solving hat on, and fast!

The initial solution

At first, you decide to implement a simple (albeit naïve) solution. You (especially experienced readers) would know that this is a good starting point before finding a more efficient solution later on. So here we go.

Starting off, all you need is an array m with 101 spaces, from m[0] to m[100]. m[i] stores the number of people who achieved i marks in their exam. Now given a range [l,r], all you need to compute is m[l] + m[l+1] + … + m[r]. So finding the sum of all values in m from l to r gives the answer.

But…

This isn’t very bad, given that m only has 100 items. But you are a visionary, so you obviously ask yourself 2 critical questions.

• What if, in the future, I’m dealing with some other array that has many more items?

• What if there are a lot of queries being asked and O(N) is too slow?

The second problem is one you’re about to face, as more and more teachers query various ranges, pushing your code to its limits. Its clear that you need a change.

A table of prefix sums

For now, while many people are querying the sum over different ranges, nobody wants to change any scores. So, you realise that you can just use pre-computation as a speed-up tactic. That means you compute what you need before hand.

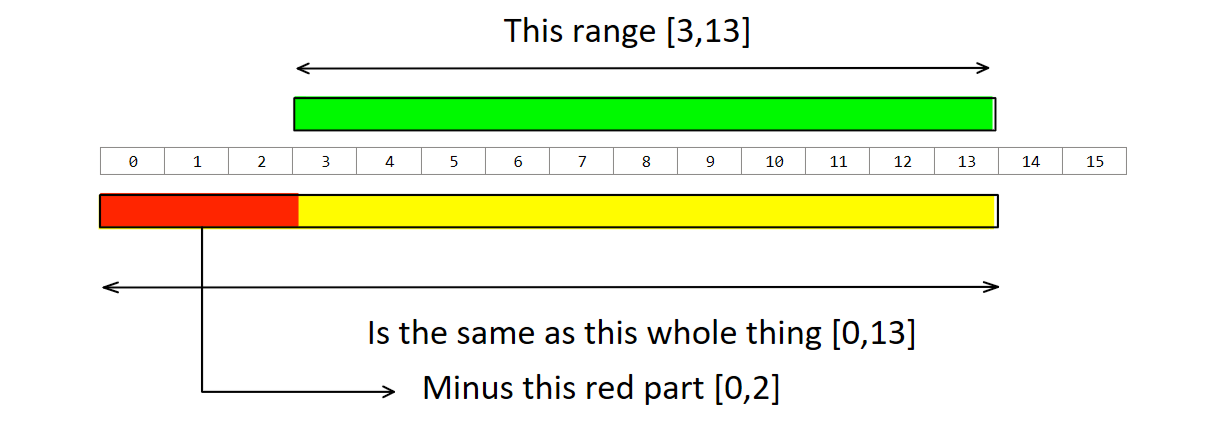
You realise that for any range [l,r], you can re-write the sum as [0,r] - [0,l-1]. An example is illustrated here.

So you create something called a prefix sum table. This is an array, p, where p[i] = m[0] + m[1] + … + m[i]. Then, you can easily calculate any range sum between [l,r] as p[r] - p[l-1].

Setting it up takes O(N), but that’s okay since every subsequent range sum can be carried out in O(1), which is a significant improvement. A single O(N) operation beats multiple O(N) operations.

p[0] = m[0]
for (int i = 1; i < n; i++) p[i] = p[i-1] + m[i];

int sum(int l, int r) {
  if (l == 0) return p[r];
  else return p[r] - p[l-1];
}

The problem

There is no problem with this solution as it is. However, the school soon approaches you saying they would like the ability to add updates to their records, especially after new exams take place. Now you have a problem.

If you want to update the prefix sum table at one index, that update would need to be propagated to every following index as well, since the range sum is changing. This takes O(N) and is incredibly inefficient. You need a faster solution.

But wait, haven’t you already got a good solution? Remember how you created a segment tree to solve a similar fast-range-updates problem before?

Range Updates

Well, there’s many problems with that solution. And that becomes apparent when the school’s cruel IT staff, jealous of your yet unmatched cognitive capacity, give your program a tight memory limit. Since the segment tree has a lot of nodes compared to the number of items in the array, the program takes too much memory to be run. But little do your enviers know that you’re smarter than them. Anyways, you were looking for a more elegant and fast data structure to solve this kind of problem, so it’s a good thing they imposed the rather draconian restrictions. To the drawing board!

A tree for every occasion

There’s a tree for every occasion. You just need to find the best way to construct the tree depending on the problem you want to solve. And a very intelligent man called Peter M Fenwick knows exactly the cure to your woes.

A picture of the smart man in question. Source: https://www.cs.auckland.ac.nz/~peter-f/

He came up with a new structure for dynamic cumulative frequency tables. You are going to explore how it works, step by step. The data structure is called a Fenwick tree. It’s named after him, and is faster than the segment tree, despite being a bit harder to understand and also being more specific. Understanding it is a step-by-step process. But the end result is very satisfying. Ready? Let’s go!

Step 1: Understanding binary

Numbers in Binary

You’ve read about binary before, but here’s a refresher anyways, to recap the important parts.

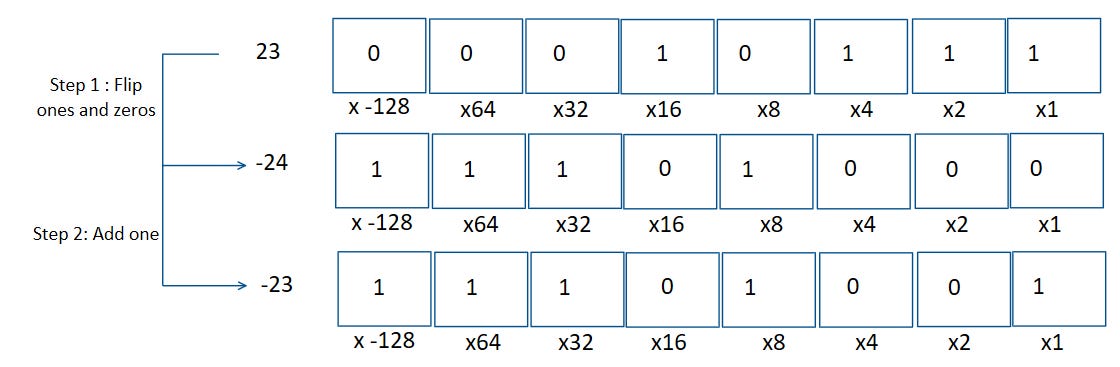
Here’s how the number 23 is written in binary.

To write -23, we flip all the digits, and then add one.

Now, if we carry out a “bitwise and” operation on the bits, we’ll notice something interesting. In a bitwise and operation, we compare 2 numbers bit-by-bit. For every bit, if they are both 1, the result will be 1. Otherwise, the result is 0.

Since we flipped all the bits, the and operation gives us zero for every bit except at the end where we added one. Let’s try this with another number, say 12.

When the bits are flipped in 12, the last 2 zeroes are made into ones. Adding one causes all the trailing ones to be converted into zeroes. So the and operation gives us 4.

By the same logic, for any number, the process of converting it into a negative number means that (k & -k) will always yield the value of the least significant bit. That is the last bit after which every digit is a zero. That was the bit in the ones place in 23, hence 23 & -23 = 1. It was the bit in the four’s place in 12, hence 12 & -12 = 4. Let us called this function L.

int L(int k) {
  return k & (-k); 
}

Step 2: A strange pattern

You decide to write down the first several values of L(k) to try and find a pattern. Sure enough, there is one.

You notice,

• Every alternate L(k) = 1

• Of the remainder, every alternate L(k) = 2

• Of the remainder of those, every alternate L(k) = 4

This is because of the math behind binary, but the pattern exists and is beautiful. It can be exploited too.

Step 3: Using the pattern

In the original prefix sum table, every space in p[i] is responsible for the range [0, i]. Now, we’re going to create a different array, called f (for “Fenwick”). f[k] is going to be responsible for a range of length L(k) that ends at k. Let’s implement that and see what happens.

The nicely colour-coded Fenwick tree is complete! Every space in the array is responsible for a small range instead of the whole thing as the previous prefix sum table. Also, instead of a tree, it’s just an array, like the prefix sum array, so you can save on memory space as well!

And here’s the fanciest thing. It’s just a segment tree with half of the nodes deleted! Instead of a left and right node, it’s just a left node. So we have 2 very cool operations we can perform.

• Suppose we are currently at index k

• At index k-L(k), we have the start of the previous range

• At index k+L(k), we have the start of the larger range that overlaps the range that f[k] is responsible for

Isn’t that cool? The array is now divided into several sub-ranges, that you can manipulate. But in order for this to make sense, we need to carry out one query and one update to see what happens.

Range sums

A fundamental misconception that must be addressed- the Fenwick tree is NOT like the segment tree! You cannot pick any arbitrary range and directly find the range sum. Remember, it is just a uniquely constructed prefix sum table. Therefore, it is used to find the sum from [0,k] in the array, not any random range. To find the sum over a range [l,r], we use the same trick as the prefix sum table.

sum(l,r) = sum(0,r) - sum(0,l-1); // l > 0

So let’s say I want the sum from 0 to some k. The process is recursive.

• Start an index “i” to keep track of our position. At first, i = k.

• Add F[k] to the running sum.

• Shift the index backwards to k - L(k). Add F[i] to the answer.

• Again, shift the index backwards to i - L(i) and add F[i] to the answer.

• Repeat until i = 0

Let’s see this in practice. Suppose we want the sum from 0 to 10.

• Start at 11

• 11 - L(11) = 10

• 10 - L(10) = 8

• 8 - L(8) = 0

• Hence F[11] + F[10] + F[8] gives the answer

Range sums

Remember how adding L(k) instead of subtracting gives us the overlapping ranges? When we update any point on the frequency prefix sum table, instead of updating everything, we only need to update the ranges that overlap the updated value. For example, let’s update F[11].

We use a similar process as previously. Notice that only the ranges that overlap with F[11] are updated. All other ranges are unaffected and hence ignored.

Time complexity

Let’s start by asking about range sum queries. We are repeatedly subtracting L(k). For every value of k, notice that subtracting L(k) is by definition setting the least significant bit to 0. Hence, k - L(k) must have at least one less significant bit than k.

This process of removing least significant bits continues till we reach 0. The maximum number of ones that we can logically remove from any number k is log(k). So the query operation has a time complexity of O(log(N)).

The case with updates is similar. The difference is this time, we are adding L(k) to k. Remember in binary, 1 + 1 = 10, so when we add L(k) to k, the value of L(k) doubles. Since L(k) describes the size of the range we’re updating, and that range is bounded by the size of the array, N, the time complexity of this operation is also O(log N).

You can verify the mathematical claims made above by checking against the table of k and L(k) provided before.

Learning points

Today you learnt a brand new data structure that allows you to check range sums quickly. You can query the sum of elements in the range [0,k] for any k in O(log N). You can update the data structure in O(log N). But of course, the problem hasn’t been completely solved just yet…

Now the school wants many more updates to be made. They want to be able to update entire ranges of marks rather than just individual marks. So until next time, you have a cool question with which to entertain your curious mind.

How do you implement range updates to the array?

You’ll read about this in part 2 next week, but see if you can figure it out before then.

---

Thanks for reading!

It’s hard work writing alone. Do you enjoy reading my work? Consider pledging a small donation of less than $10/month so I can keep writing for you.

Learn more about why your support matters and how you can help here.

Till next time… see ya!