Range Updates
The lazy concept
You woke up feeling lazy today morning.
Watching the news about the weather on TV reminds you of that problem you’ve been procrastinating. Previously you came up with a way to quickly calculate the total rainfall along a stretch of highway.
But you now want a way to update entire sections of the highway at once instead of having to update them one-by-one. This is especially since it tends to rain across a large section of the highway at a time, and so you need to implement a solution that allows updating entire ranges at once.
Hmm… laziness, procrastination. Wouldn’t it be funny if it was procrastination that would help you solve this problem?
Laziness
The concept of laziness is a unique one. Instead of updating the tree immediately, the lazy method is to delay all updates until they are absolutely necessary.
But why does laziness work in the first place? Well, it has to do with the very structure of the segment tree. And so, the idea of lazy updates occurs to you when you consider a particular range update.
While trying to understand how to speed up your solution, you run through some test cases. You imagine that the weather station informs you it has rained along cities in the range [0,4].
You need to individually update every single node along the entire array! So you highlight all the nodes that get updated.
Each node is highlighted to signify how many times it is updated.
Yellow- updated once
Blue- updated twice
Green- updated thrice
Orange- updated four times
The real problem you realise is when you try to query the amount of rainfall in that same range [0,4].
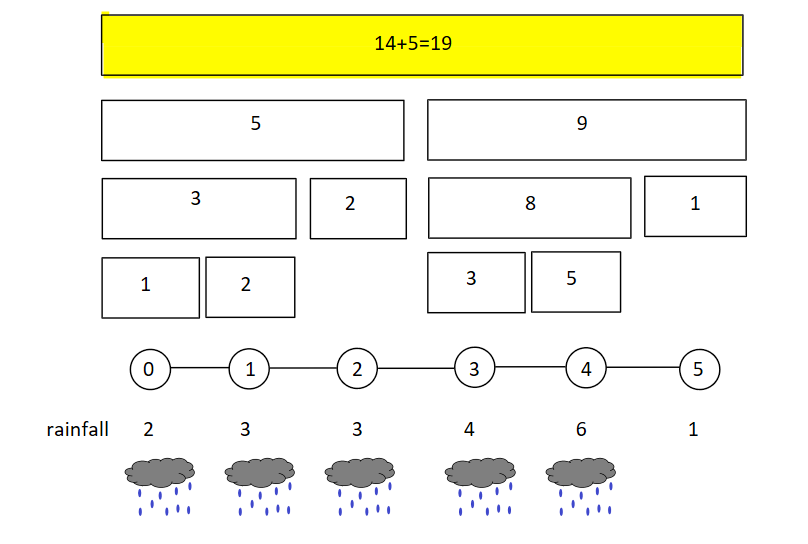
You check the children of blue nodes, ignore the red nodes, and add together the yellow nodes to get the answer. So, to find the amount of rainfall in the range [0,4], you add 8+5=13, which is your answer. You immediately notice the problem as you stare at this coloured diagram. Most of the nodes you updated earlier end up never even getting checked!
When you updated the tree, you used 19 operations. When you went to query the rainfall in the same range, you only used 5 operations. That means 19-5=14 operations were completely useless!
Bottom-up vs top-down
As you wonder how to make your algorithm faster, you spot Koshka climbing up a bookshelf and back down again. And then back up and then down again.
As you look at Koshka, your naturally curious mind imagines the bookshelf to be the segment tree and Koshka to be your algorithm. It strikes you that whenever you update the tree, it’s like Koshka climbing up the bookshelf. You start from the leaf node at the bottom and update your way to the root of the tree. But when you query for a range, you start from the root and move downward, ignoring irrelevant ranges on the way.
This inconsistency strikes you as odd. Why bother using 2 different techniques for updates and queries when you can start both from the root?
Improving the solution
Armed with your new observation, you set off to tackle the problem once again! If you start from the root node, you can achieve a logarithmic time complexity for the update operations. So, you start creating an algorithm to do this. It works the same way as querying, but updates the nodes instead.
Consider updating the same range [0,4] a second time, this time starting from the root. We know that there are a total of 5 cities in this range (0,1,2,3,4). If it rains in every one of them, we will update the rainfall for 5 cities, hence the total count in this range is increased by 5. In other words, we replace 5 individual updates with just 1 update.
Next, you move on to each child. The left child covers the range [0,2]. All 3 cities in this range are updated, so we add 3 to the value at this node. For the left node, it covers range [3,5]. We need to update range [0,4]. There’s a simple mathematical way to find the overlap: take the maximum between the 2 starting points and minimum between the 2 ending points. We get [max(0,3), min(4,5)] = [3,4] as the range to be updated. There are 2 cities in this range, so we add 2 to this node .
Since the first node was entirely within the range to be updated, we can ignore its children. This is the same logic as when we go through range queries. For the second node, we update its 2 children and stop.
That’s it! You smile as you realise you’ve found a way to update the nodes in only 5 operations! But there’s a slight issue you realise. Some of the nodes have not been updated yet!
The red nodes are all showing the wrong sums! But you realise it doesn’t matter! If you were to query the range [0,4] again, these nodes aren’t even considered.
However, these nodes could be important in some other query. But for now, you decide to mark all these nodes in red by assigning them a flag called “lazy”, to signify that in order to save steps, your algorithm has decided to be too lazy to update these nodes.
Updating lazy nodes
Lazy nodes are only updated when the need arises. For example, consider the query [0,1].
The orange node is important, but its wrong. That doesn’t matter. Since you’ve marked it as a lazy node, you can just update the value right now, and leave the node’s children alone.
It’s correct now! And you’ve managed to leave all the other red nodes alone.
Finally, you realise that the lazy flag only needs to be given to incorrect parent nodes, since you only traverse the tree from top to bottom. If you ever need to update a lazy flagged node, you can simply correct it first to remove the lazy flag, and then update it again for the actual update.
Time complexity analysis
You feel you’ve achieved a massive breakthrough with this new method. But before that, you need to analyse the time complexity of this new solution.
Since this works similarly to the range query operation, you know that you can now update entire ranges in O(log N) time complexity. Since the updates are only carried out when really needed, they are now far more efficient.
Lessons learnt
It’s really been an amazing journey discovering segment trees. You congratulate yourself on this achievement. You’d thank Koshka for her contribution too, but she’s busy chasing a mouse around the house. So for now it’s just you and the weather station again. You earn tonnes of money releasing your new solution to the country.
You’ve learnt several problem solving lessons while discovering the segment tree yourself.
Many problems are easier solved in parts rather than as a whole
Using a new perspective (top-down rather than bottom-up) can solve a problem
Counterintuitive concepts like lazy updates can actually speed up the final solution
Your solution gains popularity, and you move on to more productive endeavours. There will be no shortage of problems for a curious mind such as yourself to solve after all! But before you call it a day, you realise that segment trees are a powerful, versatile data structure. Why just use them to find the sum of numbers in a range in an array? You wonder how they can be expanded to implement other range-update operations.
Can one find the maximum or minimum number in a range instead of the sum of elements?
If the elements in the range are ones and zeroes, is there a way to range-flip? (In the range [i,j], all ones become zeroes and vice versa)
Can one use the segment tree to find the number of times an element appears in some range?
These questions continue to occupy your mind. After all, a curious coder’s brain never truly stops tinkering around, does it?
You can find the code to the segment tree here.
Thank you so much for reading! It’s hard writing alone. Consider subscribing if you’re not already a part of the community. If you are, pledge your support to my writing as an encouragement!
If you enjoyed this, feel free to share my work!
Until next time, ciao!

















Nice article and great visualizations!