Numbers in Binary
A new perspective hiding in plain sight
All numbers can be written with ones and zeroes.
That is a fact. Sounds surprising right? But it’s at the fundamentals of how computers work. But more importantly for us, it’s going to reveal a whole new way of problem solving that has been hiding in plain sight this whole time…
How is it possible?
Think about how we count in real life. Let’s run through our number to see how it’s done.
We start counting from 1, then 2, 3, 4, and so on. What happens when we reach nine? Well, we just add another digit to signify how we’ve finished counting to ten, so now we have 10. Then 11, 12, 13, and so on, all the way to 99. What next? Again, add a digit to signify we’ve reached a hundred.
We represent this using the place value system you’ve learned when you were a kid. So the number 108 is 1x100 + 0x10 + 8x1. This is called the decimal system, also known as base-10.
Now if we change it to base—2, can you guess what happens? That’s right, we start expressing numbers in powers of 2 instead of powers of 10. So instead of the place value system being in 1, 10, 100, 1000, and so on, we get 1, 2, 4, 8, and so on. The next section gives a more concrete illustration.
How do you convert to binary?
Let’s take the number 108 again and write it in base 2. See if you can spot a pattern in the steps below, and ask yourself why you think this method works.
Find the largest multiple of 2 not greater than 108. In this case, it’s 64.
108-64=44.
Find the largest multiple of 2 not greater than 44. In this case, it’s 32.
44-32=12
Find the largest multiple of 2 not greater than 12. In this case, it’s 8.
12-8=4.
Find the largest multiple of 2 not greater than 4. In this case, it’s 4.
4-4=0
Hence 108 = 64 + 32 + 8 + 4
So in binary, 108 is 1101100.
In short, we simply find the largest power of 2 not greater than the current number. Subtract that number, and repeat the steps with the remainder till you reach 0. The answer is the sum of all the powers of 2 you subtracted from the original number. Notice how in the illustration, the place values of binary numbers are labelled neatly so you can see the difference between base-2 and base-10.
Let’s do another example. Take the number 27.
Find the largest power of 2 not greater than 27. In this case, it’s 16.
27-16=11
Find the largest power of 2 not greater than 11. In this case, it’s 8.
11-8=3
Find the largest power of 2 not greater than 3. In this case, it’s 2.
3-2=1
Find the largest power of 2 not greater than 1. In this case, it’s 1.
1-1=0
Hence 27 = 16 + 8 + 2 + 1
So 27 in binary is 11011
Isn’t that simple?
Each individual one and zero is called a bit. 8 bits make a byte. 1024 bytes make a kilobyte (KB). 1024 kilobytes makes a megabyte (MB). 1024 megabytes make a gigabyte (GB) and so on.
Counting in binary looks a bit like this.
1, 10, 11, 100, 101, 110, 111, 1000, …
See the pattern?
How to write negative numbers in binary?
Yes, we can also have negatives in binary, but first, we need to do some math. This is the key to understanding why binary works the way it works.
To start off, remember that in binary we’re representing numbers as sums of powers of 2. A one represents that we include that power of 2, and a 0 means we don’t include that power of 2, and we add all the powers whose bit is 1. So if we have n bits, the largest number we can represent is if all bits are 1. This means the number will be 11111…, where 1 is repeated n times. That’s 1 + 2 + 3 + … + 2^(n-1). Why n-1 instead of n? The reason is the same logic as why the last item in an array A of length n is A[n-1]. Remember that 2^0 = 1.
Here’s how to find that largest value.
Take a moment to absorb the above maths to see what it means.
To give a concrete example, say we have the number 111. That number has 3 bits. It’s value is 1 + 2 + 4 = 7. 2^3-1 = 8-1 which is also 7. So the largest number I can represent with 3 bits is 7.
But what if I add another bit? If I add a 4th bit, its value will be 2^3 = 8. But the largest value I can represent using the other 3 bits is only 7. So what if I changed that 4th bit to be -8 instead of 8?
Then I can use that bit to represent all numbers from -8 to 7! The reason is that the number 1000 is now -8 instead of 8 since I’ve made this change. 10001 is now -8+1 = -7. 1010 is now -8 + 2 = -6, and so on till I get 1111 = -8 + 7 = -1. The number 0 is just 0, and the positive numbers only need the last 3 bits, setting the -8 bit to 0.
This concept above can be extended to all numbers!
Let the (n+1)th bit be -2^n instead of 2^n
Since the remaining n bits can represent all numbers up to 2^n - 1, you can now also represent negative numbers until -2^n
If you think mathematically about this, it makes more sense.
How to convert negative numbers into binary?
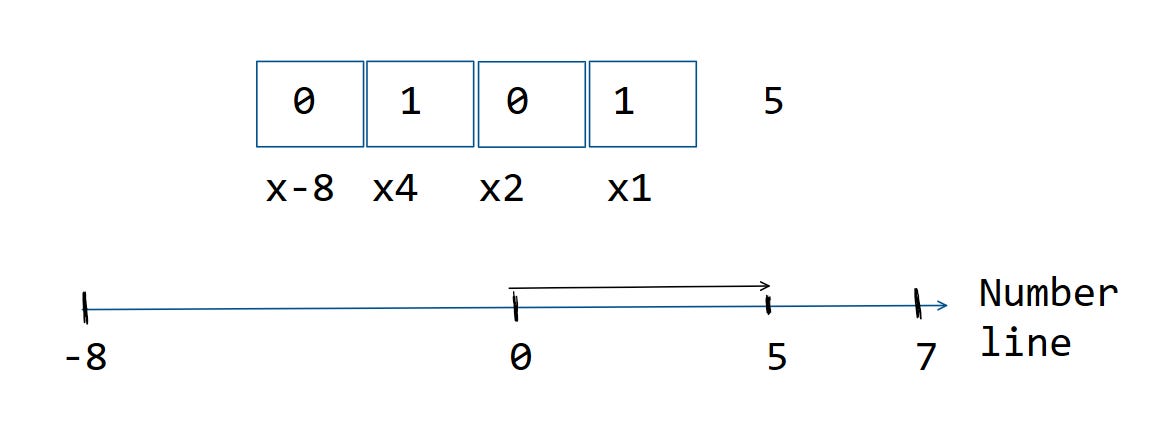
This last part of the article explains how negative numbers are converted to binary. The entire thing can be visualised on a number line. Let’s, for simplicity, keep it to only 4 bits. Say we want the number -5.
Step 1: Represent 5 in binary.
Step 2: Turn on your negative bit
Step 3: Except for the negative bit, flip all the 0 bits into one bits
Step 4: Add one to your final answer
Step 5: That’s our answer. -5 in binary is 1011 using 4 bits (this answer will change if you use more bits, the reason is the bit flipping step. Try it out and see for yourself!)
Take some time to visualise using the handy illustrations. And maybe read through the article again to ensure you understand everything. As a final exercise, give yourself some numbers to convert to binary, both positive and negative ones, to see if you really understand what’s going on and can apply it to a general case.
Hope you enjoyed today’s article. In the next one, we’ll look at bitmasks, a valuable tool in everything from combinatorics to sudoku! If you like such interesting content, do subscribe to never miss an article.
And if you’re already part of our community, share this with someone you know will enjoy it.