Road-repair works

All about spanning graphs

A road-repair company writes to you regarding a new task today.

The company wants to repair several roads across the country. The roads are in quite a bad state. You are given a map of all the cities in the country and the roads connecting them. Every road has a specific cost associated with repairing it. The company wants to come up with a way to minimise the total cost of repair, so they give a simple problem statement to you.

Select some roads to repair so that the following conditions are met.

1. The total cost of repairing all the roads is minimised

2. It is possible to travel from any city to any other city using only the repaired roads.

You’re ready to take on this challenge, so you put on your thinking cap and get to work!

Thank you for reading Elucidate: for the curious coder!

Consider subscribing to never miss a post. If you’re already part of the family, consider upgrading to a paid subscription to support my work!

Understanding the problem

You realise that this problem is a graph problem.

Introducing graphs

Immediately, you realise that you can represent the cities in the country using the vertices of the graph and the roads connecting them as edges between the vertices. You assume that the roads are bi-directional and that the graph is connected.

Definitions:

A connected graph is one where every vertex is reachable from every other vertex

This graph is a weighted one. The weight of each edge is simply the cost needed to repair that particular road.

You have the graph constructed… now what?

Spanning trees

You know that there’s a reason you’ve embarked on this task in the first place. Clearly the company could have just chosen to repair all the roads and get it over with. Your job is to remove certain edges from the graph so it remains connected.

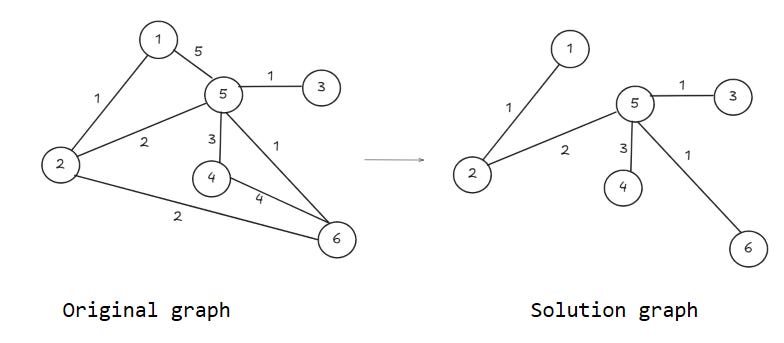
You want to keep removing edges till you arrive at the solution graph. Only the edges in the solution graph need to be repaired. You observe the properties of the solution graph.

• The sum of the weights of all edges of this graph is minimised

• It is connected

• There are no cycles in the graph

You can hence infer the following.

• The graph has minimum total weight [MINIMUM]

• It includes all the initial graph’s vertices [SPANNING]

• It is a tree [TREE]

These three properties are what define the minimum spanning tree of a graph, so congratulations on your discovery of a brand new data structure! The solution graph is called a minimum spanning tree, and now you know why it’s named that way.

Definition

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.

Source: Wikipedia

Now it’s time to actually create the MST. There’s 2 ways to do it, both relying on greedy algorithms.

Building the tree (way 1)

At first you think the simplest method is to just sort the edges in ascending order of weights. Then keep picking edges until you have covered the entire graph. That should yield the answer, right?

Not quite, but close. For simpler graphs this might work, but it ignores a very important possibility- you may create a cycle using this method. Consider the following case.

The solution generated by this algorithm is wrong because you can remove either the road connecting cities 2 and 5 or the road connecting cities 2 and 6 while still meeting the constraints set by the problem.

You need a method to detect cycles in the graph while constructing it. To do so, you experiment with a new technique. How about keep a track of which vertices have already been considered? Whenever you add an edge between 2 nodes, mark both of them as considered. Then, when you add an edge between 2 edges, simply ensure you don’t connect 2 edges already marked as considered.

It seems like that should happen, but look what goes on if you try that. The algorithm gets stuck after adding all the edges of weight 1.

There are now 2 connected components, one has the vertices 1 and 2, and the other has vertices 3, 5 and 6. Since all vertices are highlighted, these connected components cannot be connected to each other. The edges of weight 2 are ignored. So the answer is still wrong.

2 considered vertices only form a cycle if they are in the same connected component.

You now need to do 2 things to group vertices by their connected components

1. Determine if 2 vertices are in the same connected component (FIND)

2. When an edge joins 2 vertices from different connected components, the components must join to become one large connected component (UNION)

Sounds familiar? You need to use UFDS!

Author’s note

If you don’t know what a connected component is, please read the article on graphs linked earlier, or click this link.

If you need a recap, UFDS stands for union-find disjoint sets. If you have no clue what that data structure is and how it works, click the below link.

Playing with dolls

You need to create a UFDS and ensure that 2 vertices in the same connected component are never joined by an edge. That’s how you get the final solution.

This is called Kruskal’s algorithm.

Building the tree (way 2)

Your idea finally works, but you’re not completely satisfied. Think about it- implementing the entire UFDS just to check for cycles isn’t really the best method, is it?

Also what if you wanted to use an adjacency list to represent the graph instead of an edge list? That would make running Kruskal’s algorithm harder. Surely there’s a better way.

You notice that a key fact about cycles is they only form when you connect 2 vertices from the same connected component. The reason you need UFDS is to track multiple connected components. But what if you eliminate that problem by only considering one connected component at all times?

Start at any random vertex, say vertex 1 (doesn’t really matter). To ensure there’s only 1 connected component at all times, we’re only going to consider the edges connected to vertex 1. This is easy to do with an adjacency list.

To keep a sorted list of edges we want to consider, we use a priority queue. A priority queue is simply a queue that is always sorted.

Linear Data Structures

We add the edges connected to vertex 1, marking vertex 1 as considered. Now we follow a simple algorithm.

• Choose the edge in the priority queue with the lowest weight. Since the edges are sorted by weight, this is just the front of the queue

• If this edge connects 2 considered vertices, ignore it

• If it connects a considered vertex to an unconsidered one, add the edge to the answer. If the unconsidered vertex in question was v, add all edges connected to v to the priority queue. Mark v as considered

• Repeat till the priority queue is empty

Since we only consider the edges in the priority queue, and the edges in the priority queue are always from a considered vertex, we always connect a considered vertex to a not considered one, hence maintaining only 1 connected component and preventing cycles.

This is called Prim’s algorithm and it is a helpful modification to Kruskal’s algorithm.

Final words

Constructing the minimum spanning tree using the above algorithms gives the answer to the problem. But before ending this adventure, as usual, there’s a few questions.

• Which of the algorithms is better? Why?

• Can you modify the algorithms to create a maximum spanning tree instead? Can you think of situations where a maximum spanning tree could be required?

• What are the time complexities of the algorithms?

Comment the answers below. Hope you enjoyed reading this, and I’ll see you in the next one.

The source of this problem is here.