Playing with dolls
A new data structure: UFDS
Today’s problem involves a fun childhood toy- dolls!
You’re trying to teach some kids about sizes, so you decide to use these stackable dolls. Every doll has a specific size, given by some number between 1 and 500 000. Different dolls may have the same size. A doll can only be placed inside another doll if the difference in the sizes of the 2 dolls is at least 2.
At first, you have 0 dolls. Every day, you buy a new doll. You want to know, for each day, what is the largest possible number of dolls you can place in a stack?
Thank you for reading Elucidate: for the curious coder
To support my work, consider a simple contribution of less than 2 cups of coffee a month, in exchange for weekly brain workouts
Consider sharing this publication with other curious minds. The more the merrier!
Breaking down the problem
The question essentially essentially gives us an array of numbers and asks what is the longest string of numbers we can create such that no 2 numbers have a difference less than 2. The catch here is that the array is constantly changing since we keep buying a new doll every day, so we need an efficient way to solve the problem.
As is usually the case, it’s best to start small. We’ll work our way up from a naïve solution, moving slowly to a more sophisticated one, and discovering a cool new data structure on the way. Well, sort of. You see- the data structure we’re going to learn about isn’t exactly new. You already know it- it’s just being applied in a unique way.
The simplest solution
Imagine we have some array of doll sizes. Notice first of all that dolls of the same size don’t matter since we can’t stack them anyway. Therefore, only care about which sizes of dolls exist, not how many dolls of each size there are.
Here’s the second observation. Since we’re considering differences between doll sizes, it makes sense to sort the data. Anyways, we already know that sorting is a useful tool to process data faster anyways.
Finally, instead of worrying about the changing size of the array, we'll just consider the case where we’re only dealing with one array.
If there’s only one array, this becomes a special version of the longest increasing subsequence problem.
Recap
The longest increasing subsequence problem asks for the length of the longest subsequence of an array such that the elements of the subsequence are in increasing order. A subsequence of an array is an array of elements in the same relative order to each other as the original array.
For more on the increasing subsequence problem, click here
The solution works something like this.
Let’s call the array of doll sizes
a.
a = [3, 3, 1, 5, 2]sort(a)and remove all duplicate numbers
a = [1, 2, 3, 5]Now create another array
ans, that stores the answer to the problem
a = [1, 2, 3, 5]
ans = []Loop through
a. As you do so, keep a track ofans[x], whereans[x]is the last element inansLet
a[i]be the current element inathat is being consideredIf
a[i] - ans[x] >= 2, add it toans. Otherwise, ignore itfor example, i = 0 a = [1,2,3,5], a[0] = 1 ans = [] add 1 to ans ans = [1] i = 1 a = [1,2,3,5], a[1] = 2 ans = [1] 2 - 1 = 1, ignore i = 2 a = [1,2,3,5], a[2] = 3 ans = [1] add 3 to ans ans = [1,3]
By the end, the answer is what we want.
ans = [1, 3, 5]If there are N days, the time complexity of this solution is O(N^2logN). The logN factor comes because of sorting. This is not good, and we need a more effective solution. That’s where our cool new data structure comes in.
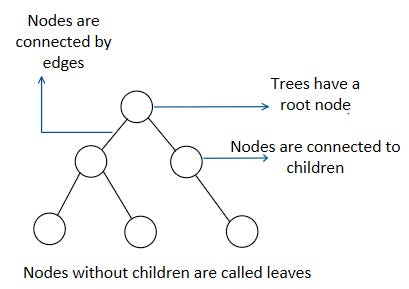
Remember graphs?
The new data structure is just a special kind of graph. In fact, we can narrow it down even further- it’s a special kind of tree.
To do this, we’re going to start by imagining doll sizes as a graph. Let’s suppose doll sizes are anywhere from 1 to 500 000 (this number can change depending on how many dolls you want). Now we’re going to imagine 500 000 independent nodes, labelled 1, 2, 3, and so on. All the nodes are considered ‘inactive’ at first. Now let’s approach the problem from another perspective.
The problem with consecutives
If you think about it, there’s only 1 thing stopping us from just stacking all the dolls into 1 stack- the fact that 2 dolls with consecutive sizes can’t be stacked together.
But consecutive doll sizes also unlock a new method to solve the problem. Imagine that we have a segment of consecutive doll sizes.
a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
ans = [1, 3, 5, 7, 9]If there are N dolls with consecutive sizes, we immediately know that the largest doll stack with only these dolls has a size ceil(N/2). Why? Because we just pick every alternate doll
Quick recap
The ceil function rounds up decimals.
ceil(2.5) = 3
If there are 2 consecutive segments, we can always just combine them.
a1 = [1, 2, 3], a2 = [5, 6, 7, 8]
ans1 = [1, 3], ans2 = [5, 7]
a = [1, 2, 3, 5, 6, 7, 8]
ans = [1, 3, 5, 7]This means we just need a way to combine dolls into groups of consecutive sizes. And our graph is just the tool
Union-Find Disjoint Sets
The new data structure is called Union-Find Disjoint Sets, or UFDS for short. To understand how it works, we need to learn the terminology in the name.
Terminology
A Set is a collection of items. The literal meaning of the English noun “set”.
Disjoint Sets refer to sets such that if an item appears in one set, it never appears in any other set
Union is an operation that takes 2 disjoint sets and combines them into one set
Find is an operation where, given an item, we determine which disjoint set it belongs to
Combining them together, we get Union-Find Disjoint Sets, or UFDS for short.
It’s helpful to take a short break from the problem at hand to really explain what’s going on with this data structure so we understand it better and can apply it to other problems.
Our data structure uses nodes to represent items. Since we’re talking about disjoint sets, every item in the set can only belong to 1 set at a time (otherwise they aren't disjoint, see definition).
So the nodes are represented in with some arrays, that contain information about each node.
Each node is represented by a number
Every node has a parent. This property helps us identify which set it belongs to. This property is stored in an array called
p.p[i]stores the parent of theith node. At first, since all the nodes are disconnected,p[i] = ifor alli. That is, every node is its own parent.Every node has a size. Technically this is an optional property, but its useful in several cases, including our doll problem, so let’s discuss it. The size of a node describes the number of nodes that call it parent. This property is stored in an array called
s. At first,s[i] = 1for alli. That is, ever node is called parent by only one node (itself).
Now we only need to find out how to implement operations like union and find. First we need to get concepts straight.
Every nodes has a parent. But this cannot go on forever. If we find the parent of this node’s parent, and then the parent’s parent, and so on, eventually we must reach a node that is its own parent, hence ending the cycle. This node is the representative of a set
This structure represents each set by a single node- the representative. That way, when we merge 2 sets, instead of having to merge every element, we only merge the representatives
To find which set an element belongs to, we only need to check the representative node
Now let’s understand what functions this data structure allows
find(i)Finds the representative of node
iWorks by repeatedly finding parents until it reaches the representative node
int find(int i) {
if (parent[i] == i) return i;
else return find(parent[i]);
}union(i,j)Takes the sets represented by the nodes
iandjand joins them togetherWorks by simply setting
parent[find(i)] = find(j)
void union(int i, int j) {
i = find(i), j = find(j); // use representatives
parent[i] = j;
size[i] += size[j];
}Let’s see how this works in the problem at hand.
Remember how we have 500 000 independent nodes yes? At first we mark all of them as inactive. This information is stored in an array active. At first, active[i] = 0 for all i, symbolising the inactive state
When we get a new doll, first check active[i]. If active[i] = 1, that means we already have a doll of this size. So we ignore this fill and move on.
Otherwise active[i] = 0. So we set active[i] to 1. Now the aim of the UFDS comes in. Sets of dolls with consecutive sizes should be in the same disjoint set. So that’s what we’re going do now.
Check active[i-1]. If it is 1, then run union(i, i-1) to merge the 2 dolls into one set. Similarly, check active[i+1] and if it is 1, run union(i, i+1).
Here’s the interesting thing though. When we run union, we can keep a live update of our answer instead of having to update it every day. Imagine that we union 2 disjoint sets of sizes s1 and s2.
At first the answer is ceil(s1/2) + ceil(s2/2). The new answer is ceil((s1+s2)/2). We can update our running answer accordingly. It’s just a matter of editing the union function a bit.
int union(int i, int j) {
i = find(i), j = find(j);
ans += ceil((size[i]+size[j])/2) - ceil(size[i]/2) - ceil(size[j]/2);
... // rest of function is as normal
}This new solution is much faster and runs in O(NlogN). Why? Well, the union and find functions have time complexity O(logN). The reason for this is left as an exercise to the reader :)
Reflection and challenge questions
This new data structure is incredibly generic. Anytime you need to classify items into disjoint sets, remember the humble UFDS
The beautiful thing about UFDS is its simplicity. It isn’t a brand new data structure. Instead, all it does is slightly extend a well known, generic data structure- the graph.
There are some weaknesses to UFDS however. For one, it can’t be used if the sets are not disjoint, that is if an item can belong to multiple sets at the same time. Also, the run time for the union and find operations is still logN, which may not be fast enough in rare cases
The children may be happy, but you aren’t. Some questions still bug your mind.
Why is the time complexity of the union and find functions
O(logN)?What other problems can you use this data structure for?
What have you learnt about problem solving in general by reading this?
Comment your answers below.
As always, thank you for reading, and I’ll see you in the next one