Range queries
Introducing segment trees
You are relaxing in your home. It’s late, and you’re watching the calm rain outside. Koshka, your cat, is accompanying you.
As you look out the window, a problem comes into your mind. Obviously, since you are a curious coder, you start wondering how to solve your problem using code. You realise that there are many cities in your country, all arranged along a straight highway. Whenever it rains, the total amount of rainfall some city has experienced increases. So a question pops into your curious head…
If I choose some stretch of the highway at any time, how can I calculate how much rain has fallen along this stretch?
In this article, we’ll explore a new data structure to solve this problem. But first, we’ll explore how to go about solving such kinds of problems in the first place. It’s going to be an adventure, let’s get started.
Formalising the problem
You get up suddenly off your chair, startling Koshka, who follows you around the house. Now that this problem has popped into your head, you aren’t going to leave it so easily, are you?
You begin getting to work with simple questions. To start off, you begin trying to represent a city in an algorithm. To generalise this problem, say there are N cities (because you want to be able to scale your code to larger highways, right?). You can label them from 0 to N-1, and place them inside an array.
Now, you can create an array called “rainfall” to store the amount of rainfall in each city. Whenever it rains, you receive an update from the weather station, and update rainfall[i] if it rained in city i. If you need to find the total rainfall along some stretch, you simply loop through it and keep a track of the sum as you go along. If it rains in city 4, add 1 to rainfall[4]. If you want to find the total amount of rainfall between cities 1 and 3, add together rainfall[1] + rainfall[2] + rainfall[3] using a for loop.
You shout, “Eureka!”. Koshka, confused by your antics, retreats to a corner of the room to mind her own business. Inspired by your intelligence, you reveal your grand invention to everybody. Is that it?
An unforeseen issue
Your solution skyrockets in popularity. Before long, you’re receiving queries from every weather station, tourist, and historian in the country! They all want to ask you how much rainfall has happened in total along some stretch of the highway. But there’s a slight problem that starts to rear its ugly head…
As the solution grows, the number of places you keep track of along the highway increases. Initially, it was just major cities, now even smaller cities and towns want in on the action. Your array now has tens of thousands of items in it. That’s no problem for a computer, though. The real problem comes when there are a hundred thousand people asking you a query every second! It’s a crisis for your computer, it simply can’t execute all the requests fast enough, and you’re forced to find a solution. Why is it so slow?
You decide to find the time complexity of your solution.
With a hundred thousand queries across ten thousand “cities” (including smaller ones) on the highway, there’s no way your computer can execute a billion operations per second! Something faster must exist.
Searching for a better idea
A good idea while brainstorming is to look at other problems. Radical new solutions to problems often arise as a result of finding similar solutions to seemingly unrelated problems.
Koshka, carelessly walking over your open computer, opens this old article, and a small detail opens your eyes:
We can solve large problems by breaking them up into smaller parts
This new knowledge inspires you, but how can you use it? First you have to read a bit more. Your reading takes you to a new data structure- a tree.
What is a tree?
Equipped with new found knowledge, a brainwave hits you- you can create a tree!
A tree is a kind of graph. A tree is any connected graph where the number of edges is exactly one less than the number of nodes. Equivalent definitions include, but are not restricted to the following.
A connected graph where there is exactly one unique path from every node to every other node.
A connected, acyclic graph
Trees have already been discussed in this article, where you learnt about decision trees. Here’s what a tree looks like.
Simple, right? But how do you use a tree to solve a complex problem like this?
Divide and conquer
In brainstorming you notice that this problem can be solved easily by dividing it into halves.
You can easily find the sum of 2 elements in the array
To find the sum of a range, you can divide it into 2 halves, and find the sum of each half
You can hence use a tree to split the array into ranges, where every node is responsible for its own range.
You smile as this stroke of genius hits you. It’s time to start implementing the solution!
Constructing the tree
Unbeknownst to you, you have just discovered something called a segment tree. You begin using your realisation to construct a divide-and-conquer solution to the problem, starting with the root node. For simplicity, you use only 6 cities, but the solution can be scaled to any number of cities.
Starting off, you create the root node, responsible for fining the total amount of rainfall across all cities.
How do you calculate this sum? Divide the array into 2 halves and find the sum of each half.
You’ve added child nodes to the root, great! Now you decide to keep going, dividing till you have the entire array split into ranges.
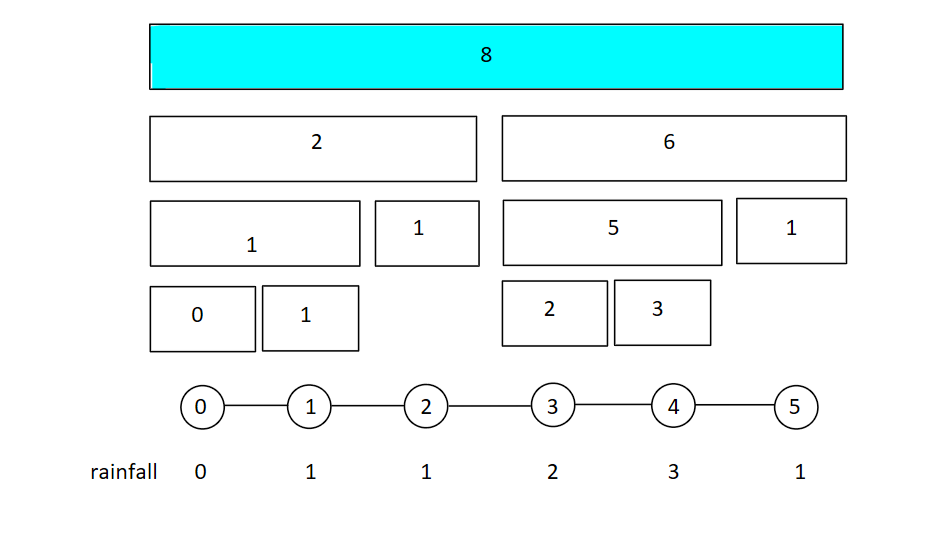
Now you realise that all the leaf nodes are responsible for only a single city. Let’s start storing the sums.
Now, time to start updating the parent nodes. Remember how each node is responsible for its 2 children? Let’s update it.
Perfect!
Finding the sum
You want to find the total rainfall between cities 1 and 4. Normally, you’d use a for loop, but here we can just use the nodes. Start at the root node.
Since you’re interested in the range [1,4]. The root node covers the entire range [0,5]. So we need a smaller range. Let’s investigate the children nodes.
These ranges are still too big, so we explore their children.
By the end, this is what the exploration looks like.
Nodes covered in red are irrelevant, and hence we ignore them. Nodes in yellow lie within the range, and we only need to consider these nodes in the final sum (1 + 1 + 3 = 5 = the answer). Nodes in blue go beyond the range, we explore their children. The uncoloured nodes are not explored at all.
At first, it’s not obvious what the advantage of this is, till you consider other ranges like the range [2,5]
You gasp at how efficient your solution is! Only 2 yellow ranges are considered, all the white and red ranges are irrelevant. What an improvement!
What if it rains?
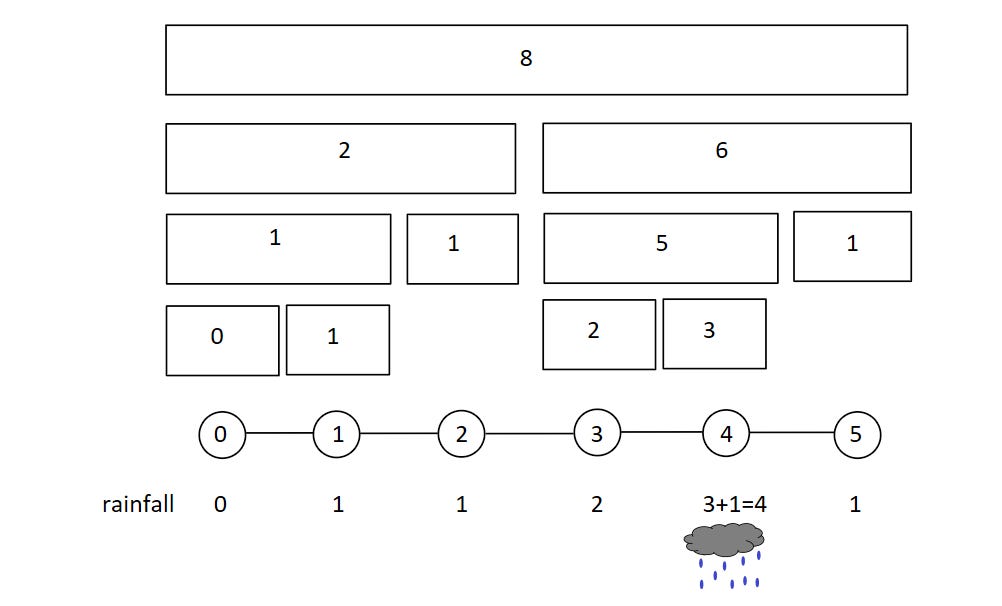
Updating is not too hard either. Assume it rains at city 4.
You find you only need to update the node and its parents. Look at the highlighted nodes to see how the change is propagated upwards.
Is it actually faster?
You recalculate the time complexities. Since you keep dividing the array in halves, the height of this tree is log(N). The logarithm is in base 2. Every update goes up log(N) levels in the tree and (on average) every query asks for log(N) levels in the tree.
log base 2 of ten thousand is around 13. You no longer need a billion operations! It’s been scaled down to just 1.3 million, far more possible for a computer to do.
But it’s not over yet!
You release your new solution, and again the entire country (at least those living on this very long highway) love it! Koshka gets excited seeing your face on the local news network.
You learnt some valuable lessons from this problem solving process! Mainly, you learnt that a problem can be solved by dividing it into smaller parts. Also, the solution to a problem may not be immediately obvious. You’ll need to explore other problems to find a solution.
But the solution you’ve found isn’t fully functional yet! It turns out that sometimes, it rains across an entire stretch of the highway at once. In this case, carrying out repeated updates has a time complexity of O(Nlog(N)), worse than the O(N) if you’d just used an array instead of a segment tree! Luckily, this isn’t happening frequently enough to disrupt your success yet. But you’re already working on the solution to this problem, to updating entire ranges at once…
If you enjoyed this adventure and want to read more, consider subscribing!
If you’re already subscribed and want to support my work, pledge your support!
If you like Elucidate: for the curious coder, share this article or the publication with others who’d enjoy reading it.
Thanks for reading, until next time!