Dynamic Programming (DP)

A new technique for when greed fails

In the previous article, we discussed greedy algorithms. To summarise, an algorithm that makes the best choice at each step is greedy, and we showed several examples of greedy algorithms and how they work, as well as how to prove their optimality.

But this isn’t always the answer. What if there is no greedy solution? What if making the best choice at one step means sacrificing the overall optimality of the algorithm? All this sounds abstract for now, but you’ll see when we go through the examples in this article, the greedy way won’t always work. We need a new problem solving paradigm, something that let’s us find the solution reliably. That’s where dynamic programming comes in!

Why being greedy fails

You can’t always have your cake and eat it too. Here’s an example problem. Try solving it the greedy way to see what happens.

Sample Problem

You want to get X dollars from a bank. When you go to withdraw the money, the banker gives you a list, A, of note denominations available. You want to withdraw the money with the fewest number of notes. How do you go about doing so?

Examples

A = [1, 2, 4, 8]

X = 10

Answer: 2

Explanation: There are only $1, $2, $4 and $8 denominations available. The best choice is $8 + $2 = $10, only 2 notes needed.

A = [1, 3, 4]

X = 6

Answer: 2

Explanation: $3 + $3 = 6.

What is the greedy solution to this problem? From what we’ve learnt, it seems like the best choice is to always choose the largest denomination right? After all, using larger denominations means we need fewer notes overall to get X dollars. But putting it into practice, we get a problem!

It works for example 1. We first choose the largest denomination, $8. We have $2 left, so we take a $2 note and we’re done. But what if we apply the same logic to the second example? We want $6. The largest denomination is $4, so we take it. For the remaining $2, we have no choice but to take $1 + $1, making 3 notes in total. But the optimal answer is to take $3 + $3 = $6, only 2 notes! So where did it go wrong?

Introducing decision trees

Before we go further, we need to talk about decision trees. As usual, I’ll put the formal definition before explaining it intuitively.

Definition:

A decision tree is a non-parametric supervised learning algorithm utilised for classification and regression tasks, organised in a hierarchical tree with a root, weighted edges, internal branches and leaves.

To understand what it means, let’s break down the meaning.

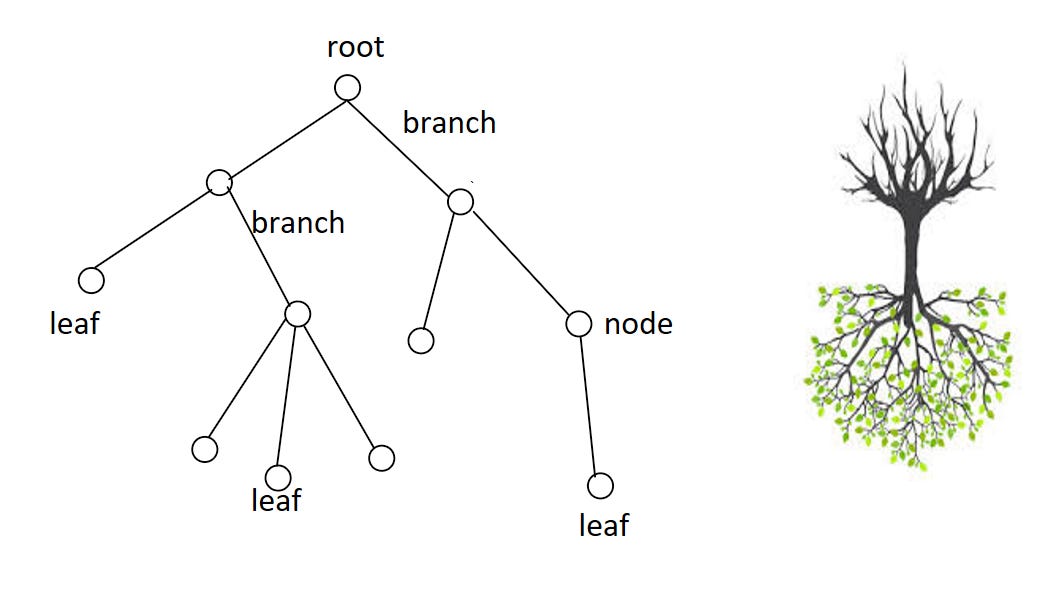
A tree is something you’ve probably seen before. Here’s a general example. Note that it looks like an upside-down version of a real-life green-and-brown tree… but just bear with me for a moment here.

Each circle is a node. Nodes are connected by branches. The first node is the root, the last nodes are leaves. We’ll explore this terminology further in my future article on graph theory. For now, let’s move on.

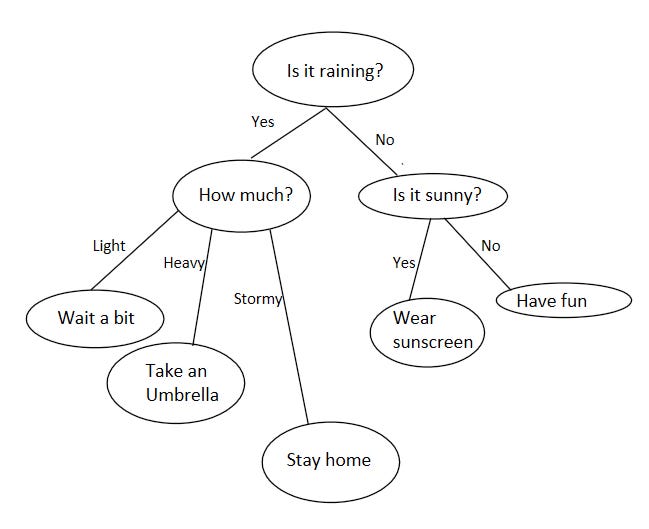
A decision tree is a tree for decisions. Here’s an example.

Makes more sense now?

• Root: “Is it raining?”

• Nodes: All circles

• Leaves: “Stay home”, “Wear sunscreen”, etc

• Edges: All lines

Problem states, transitions, and solutions

In dynamic programming (DP), the aim is to use a decision tree to solve our problem. But instead of nodes, we use something called problem states (same thing, different name). The root is called the “base state”. It’s just the information we have when we start the problem solving process. In the above example, we know nothing about the weather at the base state. Next, instead of edges, we use transitions (same thing, different name). In the transition, we ask a question about the weather (is it raining?). Depending on the answer, we take a specific path to get to the next state. In each of the next states, we now know something about the weather, and continue asking questions. Finally, instead of leaf nodes, we say we have a solution (same thing, different name). The solution here is just what we should do (wear sunscreen, take an umbrella, etc).

The rule of 3

The last introductory section before we start solving problems with DP. Whenever we attempt to solve a problem using this technique, always ask these 3 questions first. Only then can the solution materialise.

Q1: What is the transition? (What questions do I need to ask to go from one problem state to another?)

Q2: What is a state? (How do I answer the questions from the transition?)

Q3: What is the base state? (What information do I have before starting the solution?)

Once he have this, there are 3 steps to take.

Step 1: Create an N-dimensional array to store the states (we’ll explore this in more detail later).

Step 2: Fill in the base states

Step 3: Working from the base states, fill in every state till you reach the solutions.

If it sounds very theoretical and abstract, I promise it will make more sense in the examples.

Example 1: The money problem

Let’s solve the problem that started this article using DP. We’re gonna use the step-by-step solution method from above.

Q1: What is the transition?

Remember, the transitions represent problem-solving steps. In this case, it is whether we take a denomination or not. For example, do we take the $4 note, or do we leave it and take another one instead?

Q2: What is a state?

Here’s where we need to get a bit creative. How do we answer the question in the transition? In this case, every time we answer the transition question (do we take the note or leave it), what are we changing? 2 things. First, we change the number of notes we’ve taken. Second, we change the value of the money we have. So a unique state needs these 2 pieces of information. This is why we create a 2-dimensional array later on.

Q3: What’s the base state?

At the base state, we have 0 notes and 0 dollars worth of money.

Great, now to start solving the problem!

Step 1: Create a 2-dimensional array

As is convention, we’ll call our array memo.

int memo[N+1][X+1];

Here N and X are upper bounds on the size of our state. N here is the maximum number of notes we can take (we can let N=X for now). X is our target amount of money. Since taking a note can only increase the amount of money we have, we never want more than X dollars. Side note: the +1 is there to account for the index 0.

This means the state is stored in memo.

// memo[i][j] => i notes taken, we have j dollars

One question… what does this array actually store? Well, in this case it simply stores whether or not its possible to reach this state. Remember, memo is storing every state, but our decision tree may not necessarily explore all states right? So lets say,

// memo[i][j] = 1 if state(i,j) is reachable
// memo[i][j] = 0 if state(i,j) is not reachable

Step 2: Fill in the base states

What is the base state? When we have 0 notes and 0 dollars. This state is reachable as it is what we start with, so we have this.

memo[0][0] = 1; 

Step 3: Solve the problem with the transitions

Here is the C++ solution for the above problem. Remember, at every state, we choose which note to take and make a decision tree of the possibilities. Here’s the implementation in C++.

int memo[N+1][X+1];
memo[0][0] = 0;

for (int i=0; i<N; i++) {
  for (int j=0; j<X; j++) {
    if (memo[i][j] == 1) { // we can reach this state
      // for each note, construct future states
      // if we take this note
      for (x : A) memo[i+1][j+x] = 1;
    }
  }
}

// find the solution
int best_ans = 10000000; // some very big number
for (i=0; i<N; i++) {
  if (memo[i][X] == 1) {
    best_ans = min(best_ans,i);
    break;
  }
}
    

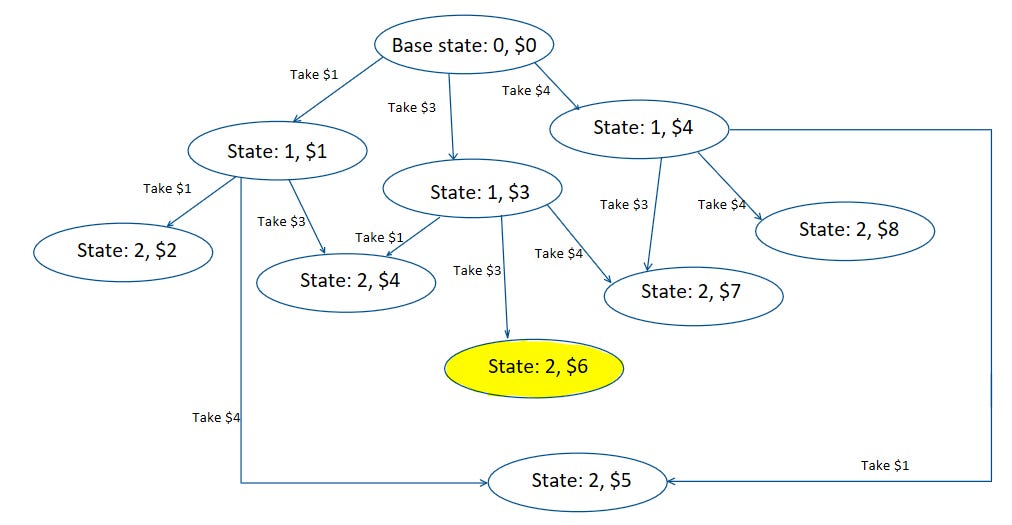
There! Looping through the memo array, for every state we can reach we construct possible future states from there. To get the final solution, we find the smallest i such that memo[i][X] == 1. Here’s a snippet of the problem’s decision tree.

Let’s look at another problem.

Example 2: Longest Increasing Subsequence (LIS)

This is a classic DP problem.

Problem:

Given an array A of integers, what is the length of the longest subsequence whose elements are in increasing order? A subsequence is some collection of elements in the same relative order as the initial array.

Example:

A = [3, 10, -2, 1, 20]

LIS length is 3 ([3, 10, 20])

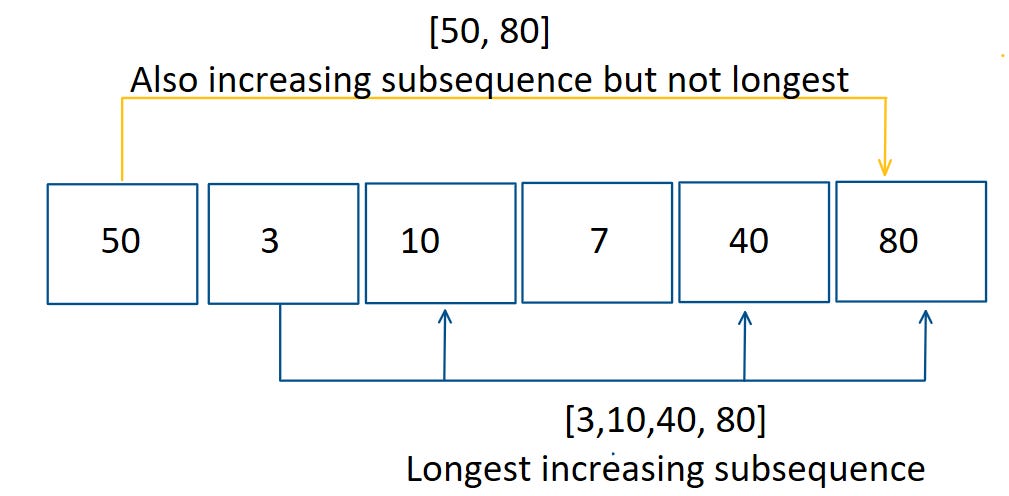
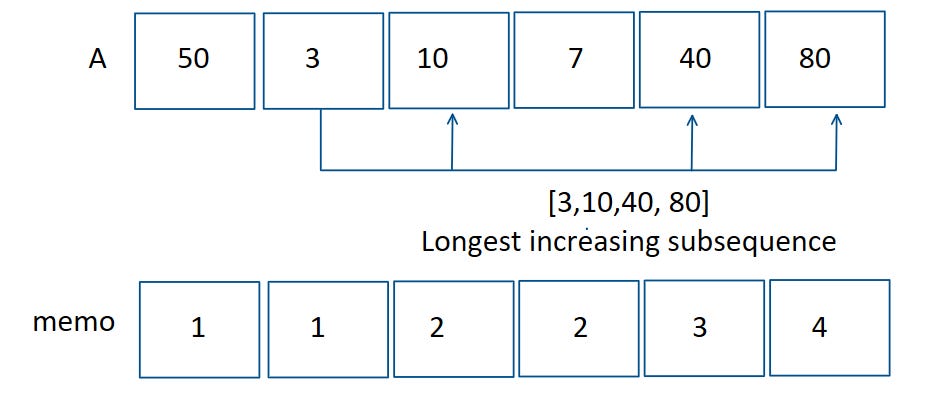
A = [50, 3, 10, 7, 40, 80]

LIS length is 4 ([3, 10, 40, 80])

Can you try to solve the problem with the steps mentioned before going ahead? Hint: there’s an observation you need to make first.

Solution

Q1: What is the transition?

Observe that if we loop through the array, then for every element we want to add it to the longest possible existing subsequence. Can you prove why this method always works?

Q2: What is a state?

Previously, in memo, we only stored whether a state was reachable or not. But we can store more information in a state! In this case, we can let the state of the problem be the index of the item we’re currently processing. We store in each state the length of the longest increasing subsequence that ends at this index.

Q3: What’s the base state?

We start at index 0. The length of the longest increasing subsequence at this point is 1 (the element itself).

Now for the solution.

Step 1: Create a 1-dimensional array

int memo[N+1]; // N is the size of the initial array

Step 2: Fill in the base state

memo[0] = 1;
// memo[i] => length of longest increasing subsequence ending at i 

Step 3: Solve the problem with the transitions

At every state, find the longest increasing subsequence we can add the element at this index to.

for (int i=1; i<N; i++) {
  for (int j=0; j<i; j++) {
    if (A[j] < A[i]) memo[i] = max(memo[i], memo[j]+1);
  }
}

In the end the answer is the largest element in memo.

Can you try to draw the decision tree for this problem?

This solution has a time complexity of O(N^2). An alternative solution: loop through every possible subsequence in O(2^N). Hence, DP is faster.

Example 3: Combinatorics

Question:

I have N boxes and want to choose K of them to take home with me. How many ways are there to do this?

Example:

N = 5, K = 2, answer = 10

N = 7, K = 1, answer = 7

N = 9, K = 4, answer = 126

Basically, the question wants us to find N choose K. Let’s denote this function as C(N,K). In this case, that’s the answer to the question.

• The transition step again needs an insight. Consider the nth box.

  • If I choose the nth box, and there are a total of k choices, I have to choose k-1 boxes from the remaining n-1 boxes. Hence, there are C(n-1,k-1) ways to do this.

  • Otherwise, I don’t choose the nth box. I now have to choose all k boxes from the remaining n-1 boxes. Hence, there are C(n-1,k) ways to do this.

  • Hence, C(n,k) = C(n-1, k-1) + C(n-1,k)

  • The transition question: should I choose the nth box or not?

• Hence our state can be 2 numbers (n, k). The state stores the answer to C(n,k). In other words, memo[n][k] = C(n,k).

• The final answer is memo[N][K]

• Base states:

  • C(n,k) = 0 if k > n (not possible to choose more than n boxes)

  • C(n,0) = 1 (exactly one way to choose no boxes at all)

int memo[N+1][K+1]; // N and K are as defined

for (int n=0; n<N; n++) {
  for(int k=0; k<K; k++) {
    if (k>n) memo[n][k] = 0;
    else if (k==0) memo[n][k] = 1;
    else memo[n][k] = memo[n-1][k-1] + memo[n-1][k];
  }
}

That’s the C++ solution.

Using DP

DP is only useful if the states overlap. There are many ways to reach every state and we’re interested in the best one. The reason DP works in this case, compared to simulating the problem directly, is that DP stores the states in a “memo”, so we don’t have to look at the same state many times. This is called “memoisation”, hence the name of the memo table. Not to be confused, by the way, with memorisation!

Conclusion

DP is a skill that is very difficult to teach. But don’t worry if you don’t get it for now. We will definitely return to continue exploring DP in the future, because its a complex topic. Once you master DP, you have mastered the hardest problem solving technique in competitive coding, good job!

Here are some DP problems to help you practice.

• https://codeforces.com/problemset/problem/1686/B

• https://codeforces.com/problemset/problem/996/A

• https://codeforces.com/problemset/problem/1466/B

Read the Codeforces editorials for each problem if you get stuck.

Challenge Problem

Problem statement:

You are in a store. You have P coins. An array A stores the prices of goods in the store. A[i] represents the price of the ith good in coins. Each good can be bought no more than once.

Since there is a sale going on, if you buy a good k that costs A[k] coins, you can choose any other good j such that A[j] < A[k] and buy that for free.

With P coins, what is the maximum number of goods you can buy?

Examples

P = 6

A = [2 4 3 5 7]

Answer: 3

(A[1] = 4, buy it. A[2] = 3, get it free. A[0] = 2, buy it.)

P = 13

A = [8, 2, 8, 2, 5]

Answer: 4

(A[4] = 5, buy it. A[3] = 2, get it free. A[0] = 8, buy it. A[1] = 2, get it free.)

Source: https://codeforces.com/problemset/problem/1282/B1.

Good luck! If you solve it, submit your solution to me :)

---

Thanks for reading! If you like this kind of engaging content, remember to subscribe to Elucidate: for the curious coder.

And do share this with friends who’d enjoy reading my work as well!

See you in the next one!