Welcome back! Today’s problem builds on what we went through in the last article. We’ll be talking about sorting pancakes.
Sounds delicious? Here’s a recap of the problem statement from before.
You have a stack of pancakes with different diameters. You can choose to place your spatula at any point along the stack of pancakes and flip the stack of pancakes until there. Write a program to find, given the diameters of a stack of pancakes, the minimum number of flips you need to get the stack sorted with the largest pancake at the bottom and the smallest one on top.
So how do you do this quickly? There’s several nuances to this problem we’ll discuss, and solving it needs us to unlock a new concept- the state space graph. So let’s dive in!
Before you continue, did you know that you can support my work for less than 2 cups of coffee a month!
Visit the homepage at https://kanaye.substack.com/ to subscribe or pledge your support and join a community of dedicated learners.
Much appreciated!
A quick recap
For a detailed explanation of the problem statement, check out the previous article linked below. Alternatively, read the recap provided in the following paragraph.
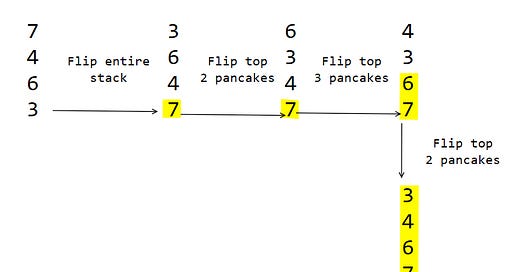
A simple pancake flipping method is illustrated here. Imagine you have a stack of pancakes with diameters 7, 4, 6, 3 respectively. The one with diameter 7 is on top. Now we can repeat this process till sorting is complete.
Flip the largest remaining pancake to the top
Flip the top pancake to its correct place
You can see the process in play below. The pancakes in the correct place are highlighted yellow.
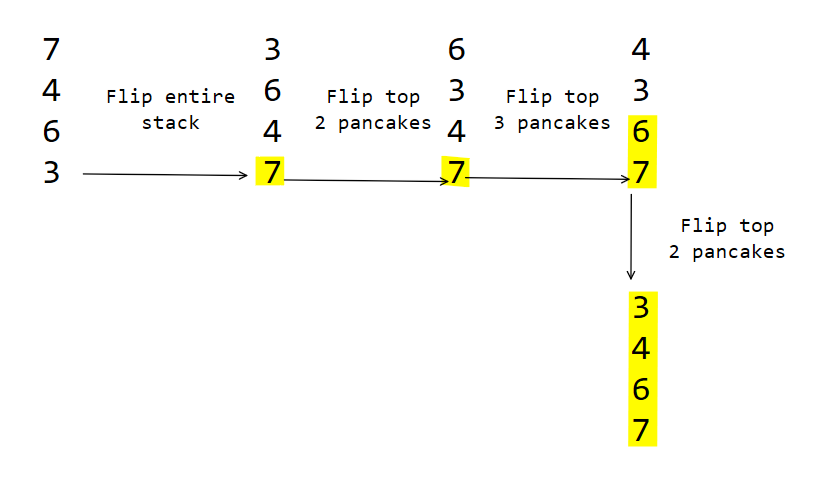
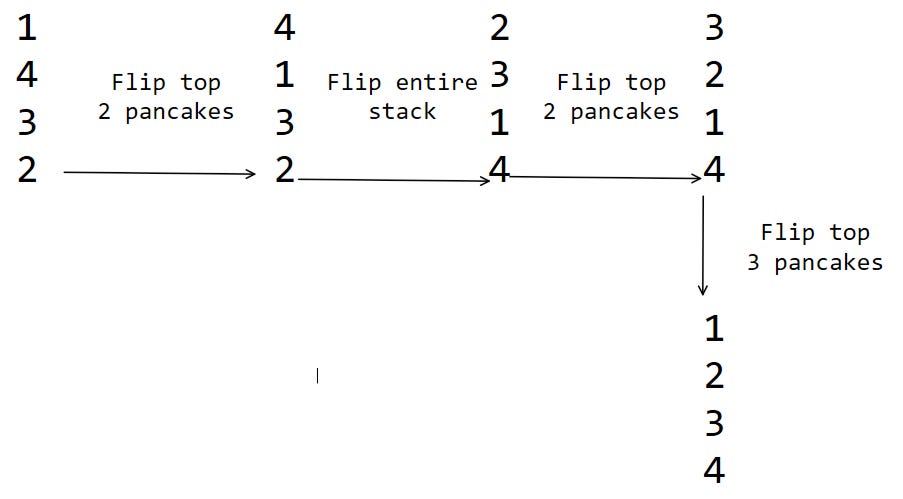
This guarantees that you can sort the list, but it’s not the fastest way to sort it. Consider the following example.
The method we have takes 4 steps. But we can actually sort the entire stack in just 3 steps.
So, how do we find the fastest method?
Exploring the state-space graph
Your stack of pancakes is still left on the kitchen platform because you are so busy thinking about how to solve this problem. But you can’t solve it yet. First you need to unlock a new problem solving dimension- the state space graph!
If you don’t yet know what a graph is, you can check it out here.
Don’t be too daunted. The state-space graph is exactly what it sounds like. Here’s how we break it down.
State: This means the state that the problem is in. A state measures how much progress we have made towards solving a problem. In this case, the state measures how close we are to a sorted stack of pancakes.
State-space: This means the space of all possible states. We want a space that describes all possible levels of how close we are to solving the problem. How do we get this? Just get every possible way that the stack can be organised. For example, let’s say our pancake stack is [2, 1, 3], with 2 on top of the stack. Then our state space is all possible ways this stack could be arranged. It consists of the following states.
2,1,3 [starting state]
2,3,1
1,2,3 [sorted- this is our target]
1,3,2
3,1,2 [reachable in 1 flip from start]
3,2,1
Every possible combination can be reached by some number of flips in some way or another.
State-space graph: A graph of the entire state space! What does this mean?
The state space contains all possible permutations in which our pancake stack can exist
A graph’s purpose is to connect these states in some way
So let us imagine a graph where every vertex represents a state, and 2 vertices are connected if it is possible to remove between them using just 1 flip.
Example: [2,3,1] and [3,2,1] are connected as it takes one flip to reach either state from the other one (flip the top 2 pancakes)
Notice that for any stack with N pancakes, there are N-1 ways to flip it (flip first 2, flip first 3, …, flip entire stack). So every vertex in our graph is connected to N-1 other vertices, where N is the number of pancakes. Now we just need to find the shortest possible path from the starting state to the target state. How do we do that?
Breadth-first Search
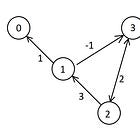
It’s very simple. Let’s say we have some graph that looks like this. We want to find the shortest path from the highlighted vertex to all other vertices.
First, we know the distance from the target vertex to itself it zero.
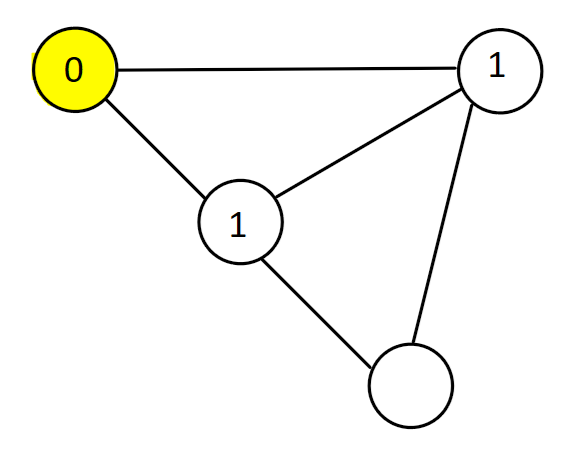
Next, we explore all possible vertices we can reach using just one edge.
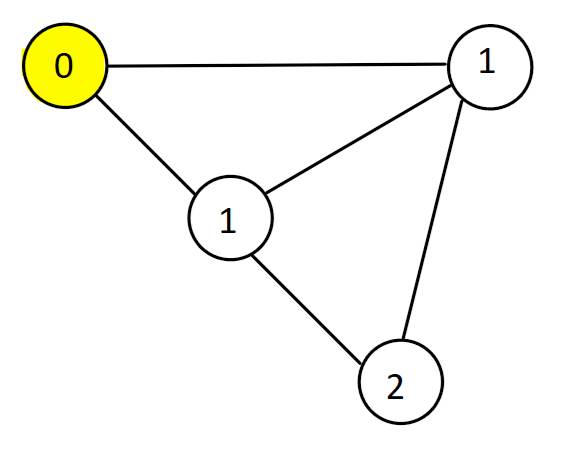
Next, we explore all possible vertices we can reach with just 2 edges.
We continue outwards till we’ve explored the entire graph and hence, we know the distance to every vertex. The time complexity of this algorithm is O(V+E), where V and E are the number of vertices and edges respectively. The exact implementation of this is not important for us right now, but we know how it works so let’s use it.
Attempt 1: Direct BFS
Once we have our state space graph, we start from the starting state (or starting vertex). Then, we run BFS to find the distance from the starting vertex to every other vertex and when completed, we query the distance to the target state. Since every edge represents one flip, we know that the distance represents the minimum number of flips we need.
There are N! states (vertices). Each vertex has N-1 connections so there are (N-1)xN! edges. So the time complexity of this is
(N-1)N! + N! = N!(N-1+1) = NxN!We can do better than this.
Attempt 2: Half BFS
This requires us to set an upper limit on the size of a stack we can sort. In this case, let’s set our limit to be N <= 10, so that our program can execute within 1 second with the time complexity we get.
Consider the state-space graph for N=10. You don’t need to do it by hand, someone else already has (see https://oeis.org/A058986). Turns out, you will never need more than 11 flips to reach the final state from any possible starting state. So that gives us a cool idea.
Notice that the number of vertices we can reach increases exponentially as we carry on the BFS. So running half of a BFS takes less than half the time, so we can do this.
Instead of starting from the start state, we start from the target state
Find all states we can reach from the target within 5 flips. This takes O(N^5)
Start a BFS from the starting state, again only going upto 5 flips.
If we encounter a state that we can reach from the target, we have our answer
Suppose we can reach some state within x flips from the target and within y flips from the starting state. Then our answer is x + y flips.
If after the BFS is finished we haven’t found any state reachable within 5 flips from the target, our answer is greater than 5+5=10. So it must be 11.
Running a BFS until 5 flips is significantly faster than running a BFS across the entire graph. The time complexity of this is O(N^5), which is significantly faster than before. And that’s it!
Final challenge
While enjoying your delicious, perfectly sorted stack of pancakes, you decide to reflect on the problem solving lessons you’ve learnt today.
You can actually shorten a BFS by only executing it halfway
You can represent problems using a state-space graph
Flipping pancakes is fun
Actually coding this state-space graph is difficult. So here’s a challenge for the readers- can you code it?
Thank you for reading! Please consider supporting my work if you enjoy these problem-solving adventures, it costs less than 2 cups of coffee a month.
Message me on Substack to submit your solution to this article’s challenge
See you in the next one!