5 fun sorting problems

100 subscriber special

I have a fun article for you guys today :)

Thanks to all you lovely dedicated readers for helping me cross this milestone! So today we’re going to enjoy a fun ride together, another fun roller-coaster. But let’s take a celebratory beak from the usual problem-solving roller-coaster and embark on a different journey. Today it’s time to create problems instead of solving them. That can be fun too! Let’s see where we end up.

This celebratory post is a throwback to my early success. My first successful article that boosted my subscribers and following was on sorting. It’s on why we can’t have faster sorting algorithms and remains, till this day, the most popular post I have ever written. Thanks again

Alejandro Piad Morffis

for that :)

A lower bound on sorting

So today, we’re going on a ride in the opposite direction. Let’s not focus on faster sorting algorithms- we’re just going to keep finding more and more weird sorting algorithms, just to see all the unique, funny ways there are to sort a list. And as an added bonus- we’ll find the time complexity of each one. Ready? Let’s go!

Join a community of dedicated problem solvers with a new article every week, just for you. Subscribe to Elucidate: for the curious coder, or pledge your support with a small financial contribution for less than 2 cups of coffee a month.

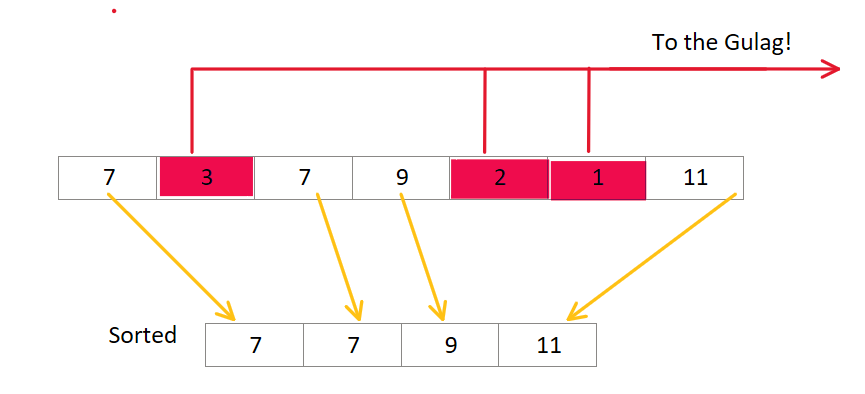
1. Stalin sort

Poster of Soviet dictator Joseph Stalin from Wikipedia

Starting off with the simplest and most ruthless sorting algorithm. Implementing this is simple. Soviet dictator Joseph Stalin has ordered the list to be sorted, so it jolly well be. Your algorithm is here to inspect that. If at any point, one of the elements of the array breaks the sorted order… it gets deleted and sent to the Gulag (metaphorically, of course).

This has a trivial time complexity of O(N).

2. Bogo sort

This sort is another simple sorting algorithm.

1. Randomly arrange the elements of the list

2. Check if it’s sorted

   1. Is it? Then we’re done!

   2. Nope? Well, go back to step 1.

It just keeps shuffling the elements of the list and checking if they’re sorted or not. So, what’s its time complexity?

There are N! ways to arrange N items of an array. Checking if they’re sorted is a simple O(N) loop. So the average time complexity of this algorithm is just O(N*N!)

3. Sleep sort

This one’s actually pretty smart, if you ignore some of its drawbacks. It’s exactly what it sounds like.

Every number in the list is given a sleep value that is determined by how big it is. For example, the number 7 is given a sleep value of 7 seconds, while 3 has a sleep value of 3 seconds. Then, we run the code in different threads so that it can execute simultaneously for all elements in the list at the same time (yes, computers can do that, but it’s too complicated to explain many details right now).

When an element is done sleeping for those many seconds, it gets added to the sorted list. Since smaller elements sleep less, they get added first. So it looks something like this.

The problem? Suppose you have the list,

[1,10000000]

It will take ten million seconds (>100 days) just to sort this, as it would wait that long before adding 10000000 to the sorted array. It also can’t sort negative numbers, or non-numerical values. And it’s significantly slower due to the unnecessary extra waiting time added.

4. Bogo-Bogo-sort

It is said that this algorithm will not sort any sizeable array before the heat death of the universe. Why?

It first bogo-sorts the first 2 elements of the array. Then, it bogo-sorts the first 3 elements of the array. Then, the first 4, and so on until complete. But, if at any iteration the bogo-sort does not sort the sub-array in the first try, it starts all over again from zero!

It’s a fun exercise to try and find the time complexity of this, so let’s try. I couldn’t really find an actual answer to this online, but since we’re recursively bogo-sorting, it should take

O(N*N!*(N-1)*(N-1)!*(N-2)*(N-2)!*…)

At least that’s what I think… but seeing other thoughts would be interesting. This one’s hard to calculate

Let’s end of with a particularly interesting one

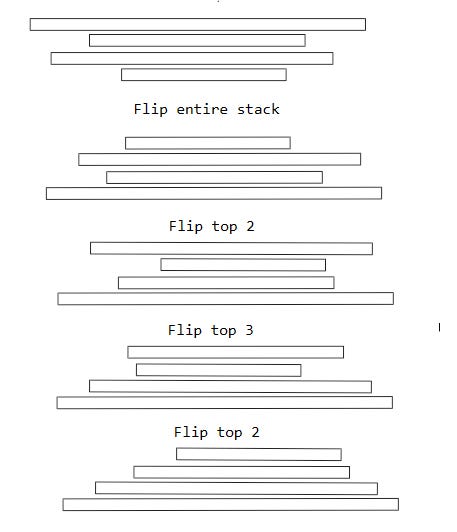
5. Pancake Sort

Imagine you have a stack of pancakes. You need to sort them. In order to sort these pancakes with the smallest one on top and biggest one below, you have a single spatula. You can place the spatula at any position, and flip the stack of pancakes up to that position.

Here’s an example.

The algorithm is simple for this one. Find the largest pancake. Flip it to the top of the stack first. Then flip it to its right position. Repeat until entire stack is sorted. What’s the time complexity of this? This always requires N operations.

This has no time complexity, since there isn’t really any way to flip an array. We could manually implement the flipping operation in O(N), which gives us a total time complexity of O(N^2). But there’s a catch.

100 subscriber special challenge

Come on, did you really think curious coders could give up on problem solving so easily? Think again.

While the pancake sort algorithm works, there is a faster way to sort it. It’s a real algorithm, a fun question to think about.

• How do you find the minimum number of operations it will take to sort a given stack of pancakes?

There is an algorithm about this, and that will be the focus of the next post, so stay tuned!

Rewards

The first 10 readers to correctly solve this problem before the article comes out next week will get to claim an exclusive free PDF reward from me! Simple head over to Substack and text me your solutions to redeem the prizes!

---

Thanks for reading!

This was a fun post. I hope you enjoyed it. Efforts are currently underway to begin paid content, so I want to hear from you.

• Comment what you would like to see in future posts and what content you would pay to read

• If you have a small, $7 to spare, head over to pledge your support for my writing

  • Find out how you can help and why your support matters

• This video below was the inspiration for this post.

Till we meet again!