Your friend has invited you to a warehouse.
This particular warehouse contains valuable paint for a large multi-national paint corporation. Your friend has received a letter from them, and he shows it to you. He’s requesting your help in solving the problem raised by the corporation.
There are 2 tasks that our company needs someone to perform, hence we have approached you.
The boxes in the warehouse need to be ordered in a way that is easy for our computers to process, but also easy for the workers at the warehouse to process
In each box, we have a paint of a specific colour. Since there are so many boxes, we have paints of every colour in the world. We need a way of ensuring that every customer gets paint of the exact colour that they want. Label the paints in a way that’s easy for our computers to process, and easy for consumers to understand.
We hope you can find a way to solve these problems for us.
Your friend is at his wit’s end, and has no idea why these very peculiar problems have been handed to him, of all people. But today is his lucky day, as a bit of research on your part reveals that all these problems are actually related to each other… the same problem all expressed in different words.
The issue with labels
You start of tackling the first problem. You need a way to label the boxes in a way easy for computers to understand. From previous research, you already know that computers understand the language of binary.
That was your first exploration into the world of base-systems. Computers represent numbers in base-2, or binary. So the logical choice for you seems to be just ordering the boxes in binary numbers right?
You start off just fine, but the problems in this approach become apparent very rapidly. You label the first box 0, the next box 1, then 10, then 11, 100, 101, 110, and so on.
The 10th box is 1010 (4 digits)
The 100th box is 1100100 (7 digits)
The 1000th box is 1111101000 (10 digits)
The 10 000th box is 10011100010000 (14 digits)
The 100 000th box is 11000011010100000 (17 digits)
The 1 000 000th box is 11110100001001000000 (20 digits)
You have a million different boxes here. What took 7 digits to represent in decimal as 1000000 took 20 binary digits to represent! That may not seem like a lot, but it’s not neat at all. The computer can process it just fine, but it’s not human friendly, and it’ll be too hard for humans to read it. So you need a way to shorten the binary into something else.
Finding a solution
In order to solve this, you need to ask a fundamental question: “What is at the root of the problem?”. You realise that the reason for this conundrum is that obviously you will need more powers of 2 to represent a number as compared to powers of 10, since 2 is smaller than 10. That’s why using base-2 needs more digits.
Searching for the solution, you need a base-system with 2 criteria met.
The base must be more than 10, to shorten the number of digits used.
The base must be a power of 2, so the computer can understand it by converting it to binary easily.
Combining 1 and 2 = “What is the smallest power of 2 greater than 10?”. The answer is 16.
Great! Now you need to find a way to actually write in base-16… oh dear. That’s a problem. There’s only 10 digits from 0-9. Base-16 needs more than digits, so what do you resort to? Well, you look it up. Turns out base-16 uses the alphabets a-f as the remaining 6 characters to form base-16 numbers.
Your friend is happy that your problem solving skills are leading somewhere productive, but he wants a better name than “base-16”. That name is “hexadecimal”. “Hexa” is the Greek prefix for the number six, and “decimal” comes from the greek “deka”, meaning 10. 6 + 10 = 16!
Hexadecimal labels
You get to work writing down the labels in hexadecimal. You start from 0, then 1, 2, 3, …, 9. What next? Use the letters! Instead of 10, write a. Then write b instead of 11. Then 12 is c, 13 is d, and so on till 15 which is f. 16 is 10 in hexadecimal. That’s a fun-fact about base-systems.
2 in base 2 is 10
10 in base 10 is 10
8 in base 8 is 10
16 in base 16 is 10
After 10 comes 11, 12, 13, …, 19, 1a, 1b, 1c, 1d, 1e, 1f, 20.
The 10th box is a (1 digit)
The 100th box is 64 (2 digits)
The 1000th box is 3e8 (3 digits)
The 10 000th box is 2710 (4 digits)
The 100 000th box is 186a0 (5 digits)
The 1 000 000th box is f4240 (5 digits)
You now have on average one less digit than the decimal representation, and a maximum of 5 digits instead of 20. What a way to save space!
Colours
But your woes aren’t quite over yet. Turns out you also need a way to represent colours. Unfortunately, there isn’t really a spectrum for colours… or is there?
So you go back to researching, and realise that every colour can be represented very simply using 3 base colours- red, blue, and green. In a computer, you’d also have to worry about a fourth attribute- opacity. But we’re not interested in that since we’re working with paint, not digital colours.
Why these 3? Well, it’s because the eye uses them as well. Each colour is represented by a certain wavelength of light. The eye can “split” colours into their component parts to determine how much of each wavelength is found in the light we see, and that determines how we see. The eye splits colours into reds, greens and blues, so it makes sense for computers to do the same thing when describing colours.
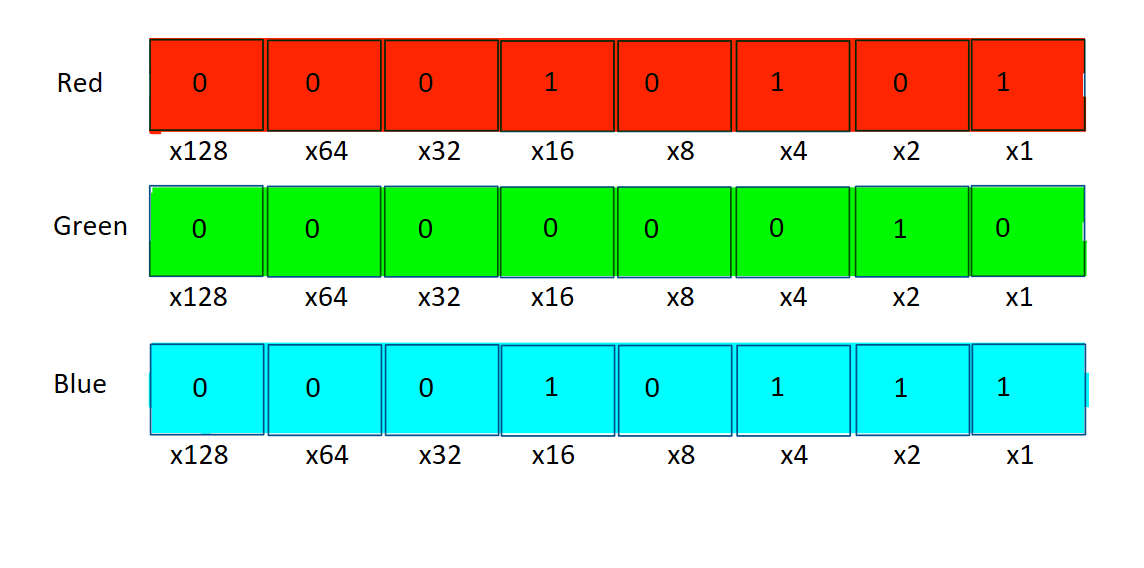
Computers use 3 numbers to determine how much red, blue and green should go into a colour.
Each colour is assigned a numerical value from 0 to 255 that determines how much of that colour is used in the creation of the final colour. For example, we yellow is green and blue, so we get this
You can also mix different amounts of red, green, and blue to get different colours.
The same problem
If you want to write out a colour in this form for a computer to understand, you’ll need 3 binary numbers. Each number can have up to 8 bits, so you need 24 bits for just one colour. Hexadecimal solves this problem by dividing the bits into groups of 4. The reason? There are 16 different values you can represent with 4 bits (1+2+4+8=15, and the 16th number is 0). Hence, you can assign each 4 binary bits a single hexadecimal digit.
Let’s explore then how we can write the purple colour we came up with in hexadecimal. First, for each number (red, green, blue), divide the number into 2 halves. Each half contains 4 bits. Next, look up the value of those 4 bits in the table above, and write its hexadecimal value below. Finally, join the hexadecimal digits into the final number.
You can see this in Google’s colour chooser as well.
You now have a way to label any paint colour in a friendly way for both computers and customers!
An interesting tale
Your friend profusely thanks you for your help designing this genius label system. But your curious coder’s mind is never satisfied, so of course you need to dig deeper.
In fact, the hexadecimal system has many interesting uses. It’s easy for humans to read, as it’s just a slight extension of the well-known decimal system (also known as the Hindu-Arabic numerals) that we use today. It’s also easy for computers to read, because all it does is divide binary numbers into groups of 4 bits (called nibbles).
Its uses extend far beyond just colours. As you used hexadecimals in the warehouse, hexadecimals are used the exact same way to label spaces in computer memory (you can think of computer memory space as a giant warehouse with many spaces). The hexadecimal is easy for humans to read, and the computer deals with it in binary.
The American Standard Code for Information Interchange (ASCII) is a set of standards that uses hexadecimal to assign every character in the English language a special value so computers know how to write symbols and emojis. ASCII is for characters in English and is a subset of Unicode- another standard for characters in languages around the world (including symbols and emojis).
Hexadecimal can also be used to represent IP addresses- special addresses that allow your network to be located on the internet. But sometimes, base-16 is not enough. For example, there are billions of videos on YouTube, and there are millions of new videos uploaded every single day. So, every video URL has a strong of 11 unique characters to identify it. How many characters does YouTube use?
The numbers from 0-9 (10 characters)
Lowercase alphabets a-z (26 characters)
Uppercase alphabets A-Z (26 characters)
Hyphen (-) and underscore (_) (2 characters)
Total: 10 + 26 + 26 + 2 = 64 characters
And 64 = 2^6, so it’s another easy number for computers to count in, dividing binary numbers into groups of 6 bits instead of groups of 4. This means more than a quintillion videos can exist on YouTube, without ever running out of URLs. That’s 1 followed by 18 zeroes!
Conclusion
You learnt some important lessons today. The first you learnt is asking that asking “Why” is often a solution to problems as it helps you get to the root of them. That’s what led you to discover the hexadecimal system. You also learnt the importance of base systems, and the magic that raising numbers to some exponent does.
Base-systems and counting systems are an important part of life, and you’ll encounter many of them. Base-10 for counting, base-60 for time, base-2 for computers, and base-16 for colours. Try coming up with your own base system, and see what kind of magic you discover by tinkering around with different bases… and another concluding question to ask- which base system is the best and why?
An intriguing matter indeed to entertain your curious mind until next time :)
Thanks for reading! I hope you enjoyed today’s post. Please support my work if you enjoy it. It’s hard work writing alone!
And ensure to share this with other curious coders who’d like to engage their minds as much as you.
See you in the next one!













Just a small note on "The 1 000 000th box is f4240 (5 digits)", 5 characters not digits. Digits are the numerals from 0 to 9.