Finding Primes
An ingenious prime checker algorithm
Another task comes your way today.
An apple farmer has came up to you with a simple problem. He and his team harvest many many apples from around the world every month. He has to decide how to divide the apples into boxes such that each box has an equal number of apples. The number of boxes doesn’t really matter, he’s just interested in dividing them equally. Sometimes, however, the number of apples he gets is a prime number. No matter how many boxes he chooses, he can’t divide them equally except by putting all the apples in one box or one apple in each box, both of which make no sense to him. The farmer wants to know, given a number of apples in advance, will he be able to divide them somehow or not?
Defining the problem
Sometimes, an easy way to answer a problem comes from looking at its definition. In this case, you check what it means to be a prime number.
Definition:
For all positive integers greater than 1, a prime number is one that has exactly 2 factors- 1 and itself. The first few primes are 2, 3, 5, 7, 11, and 13.
“Well”, you think to yourself, “that’s fairly easy to check!”. You can quickly write up a function that goes something like this…
Suppose we have a number n. Look through every number from 2 to n-1 inclusive.
Ensure that n is not divisible by any of these numbers.
If so, then n is prime. Otherwise, if n is divisible by one of these numbers, it is not prime.
But of course, it isn’t that simple.
The naïve solution fails
It’s too slow.
The farmer sends you a long list of number describing the number of apples he will get from each farm, and wants your algorithm to work on every single farm. There are thousands of farms, and since this is a super-large apple corporation, farms can produce millions of apples each month. For each number N, your algorithm runs in O(N). There are F farms, hence the time complexity is O(FN), which is simply too slow.
A new angle
Often, in order to solve a problem, you need to approach it from a new angle. In this case, the new angle relies on re-trying the same problem in a different direction.
You realise that the major slowdown is having to check whether every number is prime every single time. Since the algorithm currently has a time complexity of O(N) for every number N, that’s too slow. But there is a faster way…
Wouldn’t it be nice if, instead of having to independently check every number, we could simply have a list of prime numbers created for us, and simply check with that list to see if a number is prime or not? Sadly for you, this list isn’t ready-made, but you can construct this list easily.
Generating primes
Let’s start with an array called p. For any i, p[i] is 1 if we know that i is prime. Otherwise, p[i] = 0. Our final aim is to ensure all p[i] values are correct. This is where the sieve of Eratosthenes comes in.
The sieve of Eratosthenes is exactly that- a sieve. It filters out numbers that are not prime. So in order to create this sieve, you ask, what makes a number not prime? Let’s take it step by step.
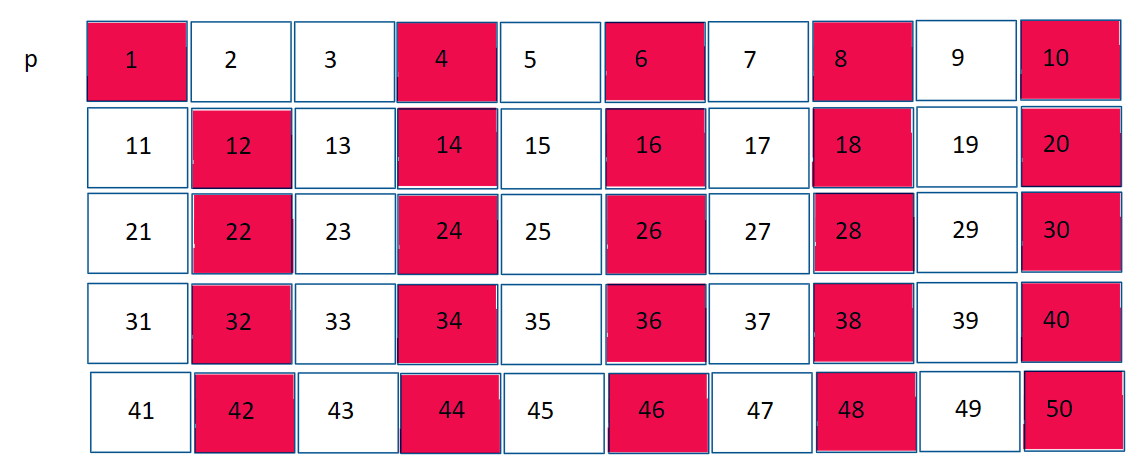
First, let’s set all p[i] = 1. We think every number is prime, since right now our sieve doesn’t know which numbers aren’t prime.
Next, we start the sieve from p[1]. Since 1 is not prime by definition, we set p[1] = 0. We then move on to p[2].
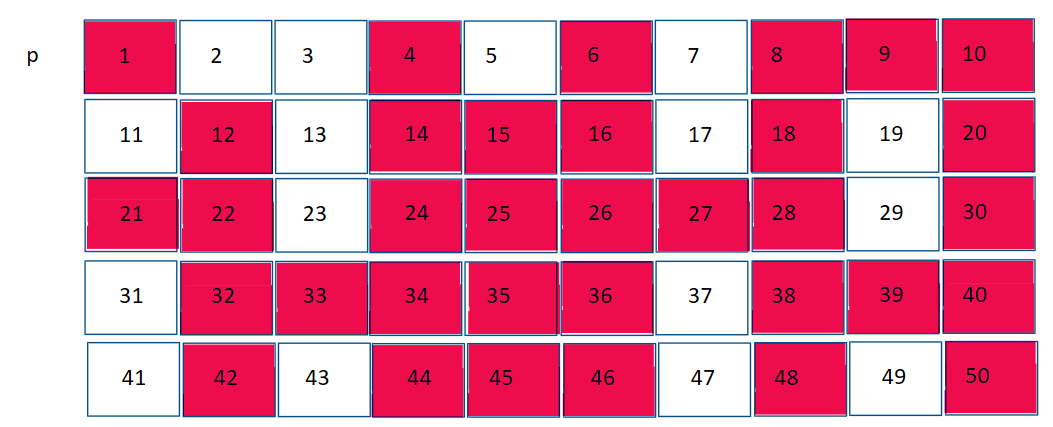
We know that 2 is prime, and it’s easy to check so as 2 is a small number. So we keep p[2] = 1. Now, you realise that every multiple of 2 is not prime. That is 4, 6, 8, and so on. Since all of these have 2 as a factor, we can sieve out all of them right now instead of individually checking each one later on. So the sieve takes that step. The sieve starts from p[4], then keeps jumping 2 spaces and marking every number as not prime. So p[4] = 0, p[6] = 0, p[8] = 0, and so on.
Now you make an observation. Since we have a sieve, all numbers from now that you encounter that are not already sieved out must be prime. Prime numbers cannot, by definition, be sieved out. So when you encounter 3, since it hasn’t been sieved yet it has no factors, hence it is prime. The same algorithm repeats for multiples of 3 that are not already sieved, getting rid of them.
The next number you see is 4, but is has already been sieved out, so you can ignore it. You move on to see number 5. 5 is not sieved, which means it is prime. You know the drill, remove every 5th number that isn’t already removed.
p[6] is ignored. p[7] is prime, so every 7th number is removed.
Suppose that p tracks all numbers till Q. We can stop at sqrt(Q), since no number less than Q can have a factor greater than sqrt(Q) without also having a factor less than sqrt(Q). Why? Multiplying 2 numbers greater than sqrt(Q) gives a number greater than Q, which is outside the range that p tracks. In this case, Q = 50. sqrt(Q) is around 7, so we can stop at 7.
And hence, the sieve has worked. You can check whether any number is prime now in O(1) by simply querying p[N].
Time complexity analysis
Now, we have an array p that can easily determine if a number is prime or not. Let’s consider the time complexity of this algorithm.
For any prime number x that is encountered, every x-th number in p is sieved out. Since there are Q numbers in p, this step has a time complexity of O(Q/x).
This is repeated for every prime number x. So we now need the sum of reciprocals of primes until Q.
The proof for this is too complex to be included here, but you can look it up on Wikipedia.
Now for all the F farms, we can answer our problem in O(1). This gives us a much better final time complexity.
Where Q is the largest number of apples that any farm can make. This is far more efficient.
You may notice that one last thing. Since we’re only considering primes till sqrt(Q), shouldn’t the sum of reciprocals be log(log(sqrt(Q)) instead of log(log(Q))? Well, no. Because we remove constants in big O notation.
Conclusion
This technique is an example of dynamic programming, which you may recall from before. Our base state: marking the first prime number 2. From there we build onto more states by checking if a number is prime or not, and if it is removing its factors.
You managed to save a lot of time. However, this is also a new problem-solving technique, called precomputation.
Precomputation:
Sometimes, problems can be easier solved if important information is all computed at once at the beginning rather than individually recalculated again and again later on.
Here, computing the list of all prime numbers saves a lot of time now, as it prevents re-computations later on.
You’re happy you’ve helped yet another person with your problem solving skills, and the farmer gives you a box of apples as a reward for your hard work.
The sieve of Eratosthenes is a very ancient algorithm for finding prime numbers. But it has other uses as well. It turns out you can modify the sieve slightly to track the number of prime factors of a number rather than just whether it is prime or not. Can you figure out how? Hint: it involves changing something in p…
Thanks for reading this post! It’s hard work writing alone… please consider supporting my work if you want a new brain-stimulating article every week.













nicely covered
Thanks!