The vector is one of the most fundamental data structures in coding. But here’s a thought that may not have crossed your mind. We can represent some vectors as a single number! This is the underlying concept behind a bitmask, and will be the focus of this article. But before going on, consider subscribing if you’re a curious coder who likes this kind of content.
Preliminary: What are binary operations?
Binary operations are operations we perform on ones and zeroes. There are several kinds of binary operators, and we’ll go through them one by one. They are quite simple and like many things coding, are exactly what they sound like.
Bitwise And
This uses the & operator. It takes 2 bits and returns 1 if both bits are 1.
0 & 0 = 0
0 & 1 = 1 & 0 = 0
1 & 1 = 1
Bitwise Or
This uses the | operator. It takes 2 bits and returns 1 if either bit is 1.
0 | 0 = 0
0 | 1 = 1 | 0 = 1
1 | 1 = 1
Bitwise Xor (Exclusive Or)
This uses the ^ operator. It takes 2 bits and returns 1 if either bit is one, but not if both bits are one.
0 ^ 0 = 0
1 ^ 0 = 0 ^ 1 = 1
1 ^ 1 = 0
Bitwise Not
This uses the ~ operator. It only takes 1 bit, and flips it.
~ 0 = 1
~ 1 = 0
Left/right Bitshift
Shifts bits to the right or left.
This uses the << operator. It shifts a sequence of bits to the left, equivalent to multiplying by 2.
1 << 1 = 10
10 << 1 = 100
10 << 2 = 1000
This uses the >> operator. It shifts a sequence of bits to the right, equivalent to dividing by 2 and dropping any remainder.
1100 >> 1 = 110
110 >> 2 = 1
1 >> 1 = 0
Binary representations of numbers
Recall from the last article, every number can be represented as just ones and zeroes. In fact this is how computers actually represent numbers. Because of this, we make some invaluable observations.
Observation 1
Any number can be represented as a vector of ones and zeroes using its binary representation
Observation 2
Ones and zeroes can be used to represent any 2 distinct values (like true and false, male and female, present and absent, etc)
Conclusion
Any vector that contains 2 distinct kinds of values can be represented as a single number!
This might seem very abstract for now, so I’ll explain them in more detail before moving to an example problem.
Whenever we write a number, the computer automatically interprets it as a string of ones and zeroes. In most cases, this doesn’t actually affect our code. But the idea of bitmasks is to manipulate this fact.
All integers in the computer take up a fixed amount of space. For example a C++ integer always takes up 16 bits. A long integer takes 32 bits and a long long integer takes up 64 bits. In competitive coding, we use long long for convenience so we can deal with large numbers.
Bitmasks: Bing AI illustrates its perspective
In other words, using the long long integer data type means a number is the same thing as a vector consisting of exactly 64 ones and zeroes. We can actually do several cool things with this, but for now I want to scale it down. Let’s just say we have 8 bits instead. The examples I give can be scaled up to any number of bits, but we’ll work with 8 for ease of illustration.
What can I do with bitmasks?
Let’s say our bitmask is 00010101 (the number 21). Here are some operations we can do to our bitmask. If you think of it as a vector of integers, it becomes easier to understand why these operations are useful.
To create the bitmask, just declare an integer variable.
int bm = 21;
If we want to “set” the ith bit (make the ith bit 1), we use the bitwise or operator.
bm = bm | (1 << i)
Say we’re setting the bit at position 1 (remember, we’re counting from right to left here because of how binary works).
The bitwise or operator performs a bitwise or operation on each bit of the 2 numbers. Notice that all other bits remain the same, look through the operation description in the previous section again to see why.
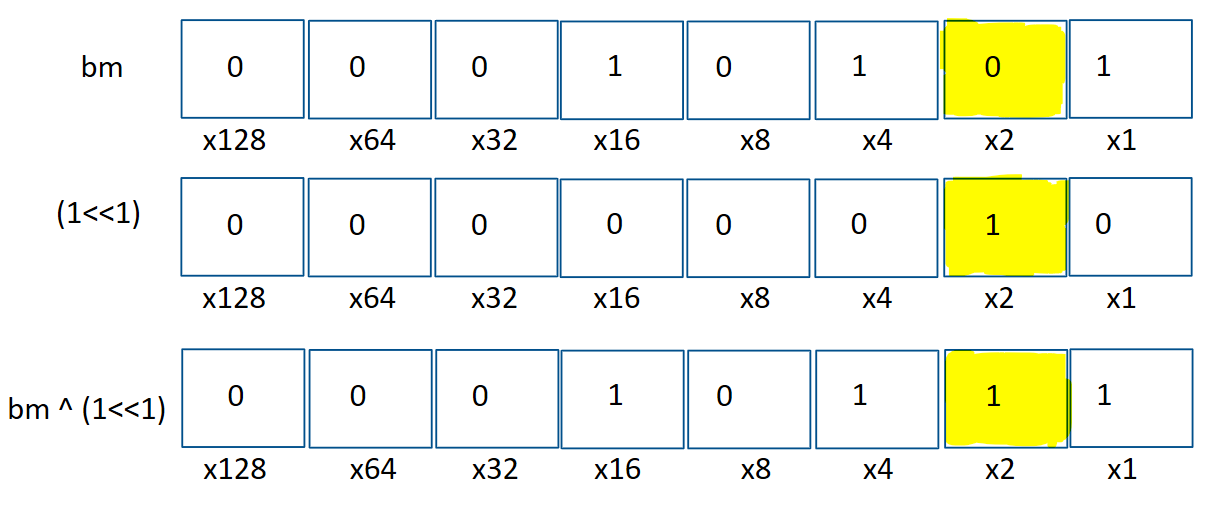
If we want to “toggle” the ith bit (make the ith bit 0 if it’s 1 and 1 if it’s 0), we use the bitwise xor operator.
bm = bm ^ (1 << i)
Let’s take our modified bm from above and toggle the bit at position 1. Let’s see how that plays out.
See how the xor operation, when carried out on every bit, has this effect? The other bits remain unchanged! If we toggle the bit again,
If we want to “clear” the ith bit (make the ith bit 0), we use the and and not operators.
bm = bm & ~(1<<i)
The bitwise not operator flips all the bits of 1 << i. Hence Let’s clear the bit at position 2 of our bitmask right now.
Notice how all other bits remain unchanged! Try to go through this and see why that happens.
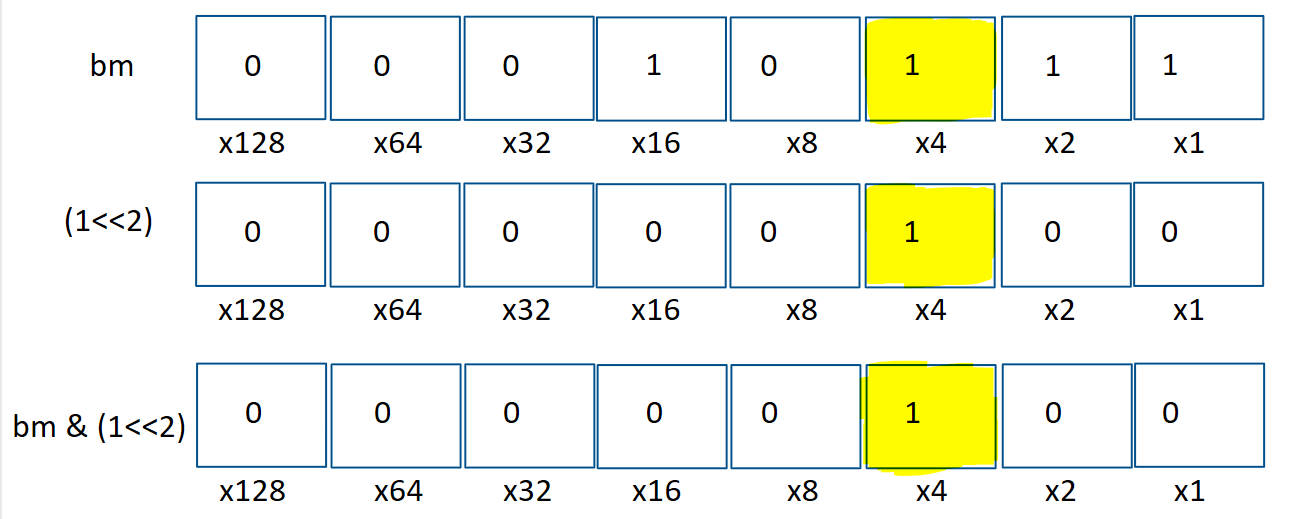
To check the value of the first bit, use the and operator
bm & (1 << i)
Let’s, take our bitmask, now back to its original since we turned the bit at position 1 on and then off again. Say we want to check if the bit at position 2 is on.
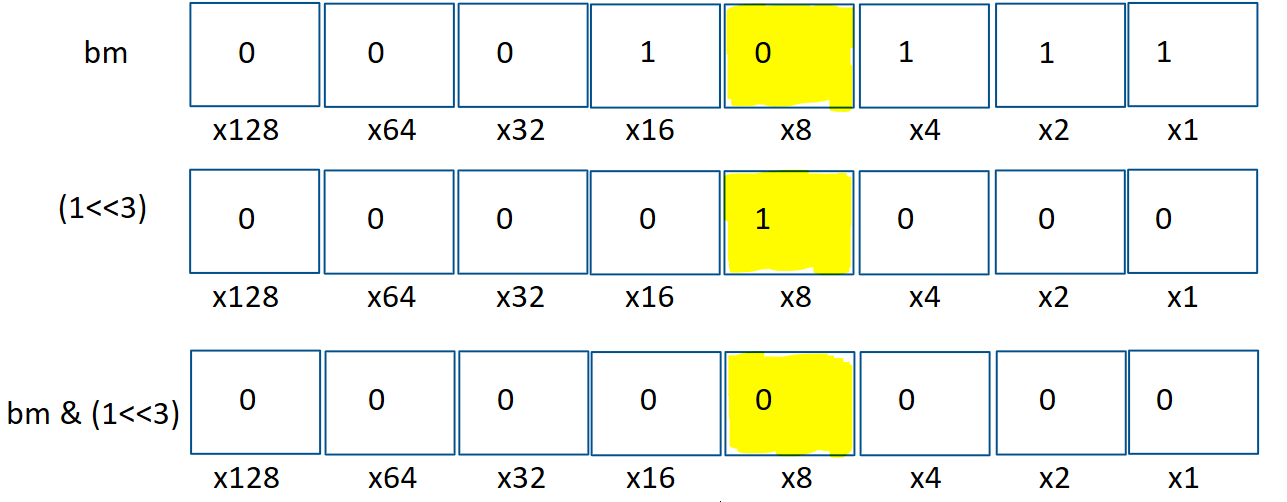
Notice that if that bit were 0, then our and operation would have just given the number 0 instead. To illustrate, let’s try checking if the bit at position 3 is 1.
So this operation returns 0 if the ith bit is 0, otherwise it returns 1 << i.
Finally, we talk about 2 special bitmasks
To clear all bits of the bitmask, set it to 0
bm = 0
Because 0 in binary is just 00000…
To set all bits of a bitmask of size n (we only want to use the first n bits), use 2^n - 1
bm = (1<<n) - 1
The math behind this can be explained in 2 ways.
It’s the same reason 10000 - 1 = 9999 and 100 - 1 = 99 in the normal decimal counting system humans use.
It has to do with the largest value of n positive bits, see the previous article for a recap.
NOTE:
In the above illustrations the last bit represents 128 instead of -128
In actual case, unless you’re using unsigned integers, the last bit is negative. This is completely unimportant for the above examples because we don’t need negative numbers, but it has other implications I will discuss in a future article.
For now, we can just move on.
Bitmasks have one important limitation: their size.
A bitmask cannot represent a vector of length greater than 64.
In actuality, bitmasks are usually not used for vectors of length greater than about 25 because many problems need us to loop through bitmasks, and 2^25 is already a very large number of operations for the computer to perform.
A bitmask cannot be used for vectors with more than 2 types of values in them
But they are very useful nonetheless, as we’ll see soon.
Let’s try to solve the following problem for the rest of the article
You have n books, labelled from 0 to n-1. Reading book i takes t[i] minutes and gives you e[i] experience. So your task is to find out, which books should you read to get at least 100 experience in the least amount of time?
You are given that n < 20, t[i] < 10^6 and e[i] <= 100 for all i
For example, say that there are 7 books as given below
The best way is to read books is books 4 and 5 which will give you 83+67=150 experience with reading time 150+75=225 minutes. Another way to read the books is to read books 0 and 5, which takes only 175 minutes to read but gives 88 experience, which is not enough and hence this is not a valid solution.
Try to think about how you would solve this problem before reading further. For the purpose of this article specifically, we want to use bitmasks to solve this.
The solution
One possible bitmask representation of data is to let a 1 signify that we read the book at this position, and a 0 represents that we do not read this book.
For example, the bitmask 0000001 means we only read book 0, while the bitmask 0101000 means we only read books 3 and 5.
We want to loop through all possible bitmasks. Recall that if we have n bits in our bitmask, the largest value I can represent is 2^n - 1. Think about the following statement
If we loop through all numbers from 0 to 2^n - 1, we have covered every possible bitmask from 0000... to 1111...
In our example, n=7. So we want all bitmasks from 0000000 to 1111111.
The number 0 represents the bitmask 0000000
The number 127 represents the bitmask 1111111
So we only need to loop through all numbers from 0 to 127 inclusive to loop through all possible bitmasks
For every bitmask, we loop through the bitmask and check which bits are 1. The positions represent the books we read. We loop through the bitmask to check the total experience and reading time of this combination of books we choose to read.
We keep a running track of the best bitmask, updating as we go along.
Once the algorithm is completed we should have our answer
Bitmasks have many more beautiful applications, and they will definitely appear more in future articles. In the meantime, read through this one again to ensure you fully get this data structure. Try to code a solution to the example problem as well (I’ll post my code soon). But that’s all for now, goodbye!
I hope you enjoyed reading this. If you’re a curious coder like me who enjoys new learning every day, subscribe to stay updated to new articles I write.
And if you know a fellow curious coder, get them to join too. The more, the merrier!
