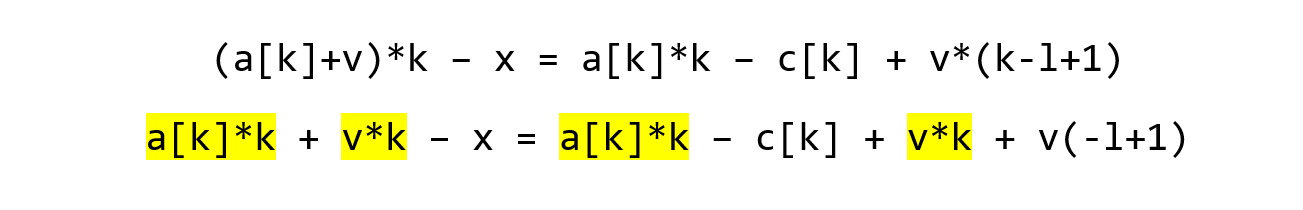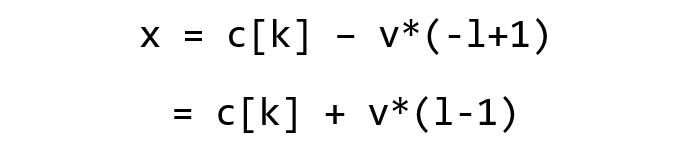Previously, you found a cool data structure for fast range sums. This time, you want to develop a similar data structure for range updates. This will lead to a key insight through which you can combine them to form a data structure for fast range sums and updates. But first, a little recap…
Thank you for reading Elucidate: for the curious coder.
Your support is crucial to keep the newsletter running. Click here to find out how to support my writing.
Click the button below to subscribe, or to pledge your support if you’re already a subscriber.
Recap: the Fenwick tree
A Fenwick tree is just an array, f. It is responsible for an array a. We also define a function, called L, whose exact definition isn’t important for now.
f[k] is responsible for the sum of elements from a[k-L(k)+1] to a[k]. To find the sum of all elements from a[1] to a[k] (using 1-based indexing), we start from f[k] and repeatedly subtract L(k), adding the value at f every time. This process is illustrated below.
We also discover that if you want to update a value, a[i], all the indices in f that overlap with a[i] can be updated with a similar process, but we add L(i) instead of subtracting. Again, it is illustrated below.
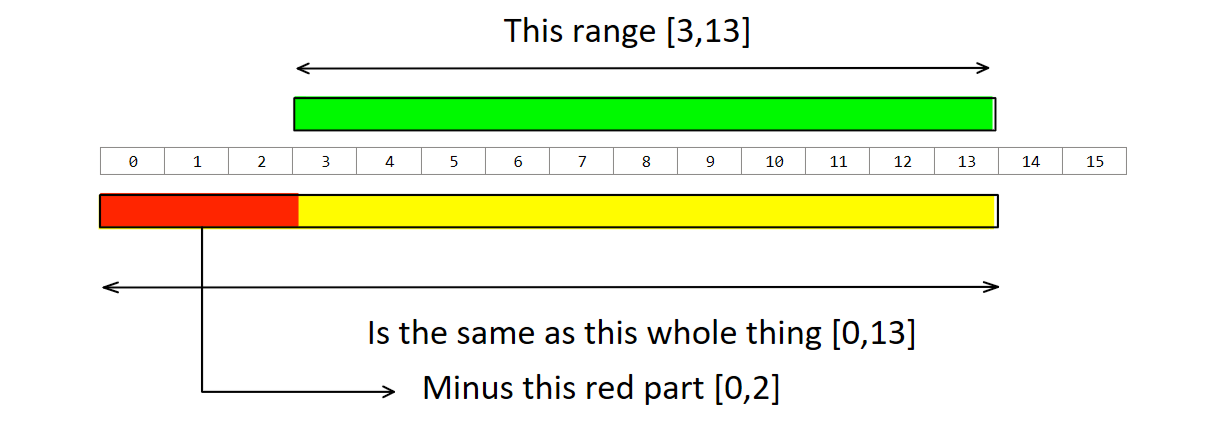
In summary, the Fenwick tree let’s us rapidly calculate the sum of elements from a[1] to a[k] for any array a. It also let’s us update values at a point. Both operations take O(log N), where N is the size of A. If we want the sum of all elements in a within a range, [l,r], we simply take the sum of the range [1,r] and subtract the sum of range [1,l-1]. This is also illustrated below with an example.
Both sums can be found in O(log N) as explained earlier.
For more detail, see the previous post.
With that out of the way, it’s time to find out what a difference array is.
Understanding problem requirements
A difference array is exactly what it sounds like. It stores differences. This is best understood with an example. For today’s example problem, your job is very easy. You have N buckets of water in a straight line, labelled from 1 to N. Every day, a stranger will choose some volume of water v. He will then select a range of buckets, [l,r]. Now, he adds exactly v litres of water in every bucket starting from bucket l and ending at bucket r. Your job is to figure out on any day, how many litres of water are there in one specific bucket?
To do this, you make a list of what you need.
The ability to add to entire ranges at once (range updates)
The ability to query the amount of water in one bucket (point query).
You don’t need to query the sum across any range in this problem, so the Fenwick tree isn’t what you’re looking for exactly. So you get to work devising a clever new data structure instead.
The difference array
This is best understood with a concrete example. Let’s suppose the buckets have some amounts of water already. We’ll keep an array a, where a[k] stores the amount of water in the k-th bucket.
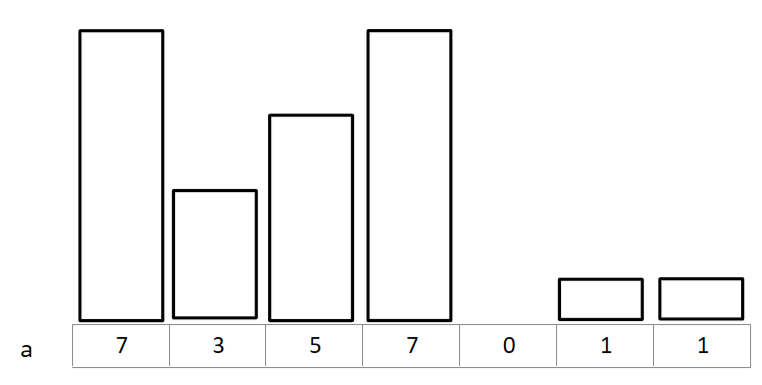
Now we’re going to create a difference array. Let’s call it d, for difference. d[k] stores a[k] - a[k-1]. d[1] = a[1] (we’re using 1-based indexing for consistency). Here is the difference array for a, colour coded for
Notice that if you add up all the elements from d[1] to d[k], you’ll get a[k]. You can try this yourself. d[1] + d[2] + d[3] = 7-4+2 = 5 = a[3]. This should make intuitive sense. If you know the starting element, and the difference between every 2 consecutive elements, then you can add these differences to find any nth element.
Now let’s look at some magic we can do with difference arrays that allows range updates.
A unique property.
You realise that if you update an entire range, [l,r], by adding some constant value v, the difference between 2 elements in that range does not change! Why? Because you’re adding a the same value to every number. So mathematically, the difference remains the same. The only changes are at the edge of the range. To understand this, let’s consider a concrete example. In our previous array, let’s say we want to update the range [3,5] by adding 2 to each number in the range. Look at how this impacts the array.
Examine it step by step. For spaces less than l, nothing happens. At d[l], notice that a[l] is increased by 2 while a[l-1] is unchanged. So the difference increases by the amount of the updated, in this case, +2. Between l and r, since all items are increased by the same amount, there is no change. Since r is increased by 2, while r+1 remains unchanged, d[r+1] is decreased by 2. Think about the maths…
Isn’t that easy! Now we know that a range update is very simple. To increment all elements in range [l,r] by some value v, simply execute 2 steps.
d[l] = d[l] + v
d[r+1] = d[r+1] - v
Now, we know that to actually find a[k], we need to find the sum of all elements from d[1] to d[k]. How to do this? We use the Fenwick tree for fast range sums! So d can be stored as a Fenwick tree which we discussed earlier. Now we have range increments and point queries in O(log N) each.
What about summation?
This is the final, coolest part, the grand finale of the whole exploration- fast range sums!
When you update a, observe how the sum of elements from a[1] to a[k] changes for all k.
In general, there are 3 kinds of indices. If we increment the range [l,r] by value v, then
For all k < l, the sum is not affected
For l <= k <= r, the sum is increased by v*(k-l+1)
For k > r, the sum is increased by v*(r-l+1)
Check it out yourself. This should make intuitive sense again, if you look at the illustration.
Now, we currently store a difference array, using which we can find a[k] in O(log N) and we can also update ranges in O(log N). Now, how do we find the sum of all elements from a[1] to a[k]?
To do this, let’s assume that the sum is equal to a[k]*k - c[k]. Here, c[k] is a correction value that we keep track of, since the sum is not actually a[k]*k. Our job is to just track this correction value.
When we initialise c, we manually track the difference between the actual sums and a[k]*k, and update c accordingly. Now, we need a way to update the correction values for every update. And we can do this using maths.
Let’s look back at the increment of any range [l,r] by v. When we update c[k], we need to consider all 3 cases.
Case 1: k < l
As already discussed, the sum is not changed for these values of k, as the index is less than the start of the update range. So, we can ignore all k < l.
Case 2: l <= k <= r
For this range, let’s use maths to calculate the value. Let’s call our new correction value x.
At first, our sum is a[k]*k - c[k]. After the update, the sum is increased by v*(k-l+1), as we’ve seen. That gives us the new sum, which we plan to calculate using (a[k]+v)*k - x. a[k]+v is the new value of a[k], and x is the updated correction value. Our job becomes to solve for x.
Let’s expand this equation.
We have 2 common terms that we can cancel out. That simplifies the equation
Multiply both sides by -1 and re-write the terms, and we get this.
So for all k between l and r, we need to increase c[k] by v*(l-1).
We only have one scenario left.
Case 3: k > r
Here, the sums are updated by a constant value, v*(r-l+1). So we do the same thing. But a[k] does not change, so our new sum is a[k]*k - x.
Again, we increase the correction values by v*(l-1), but now we also have to subtract v*r to balance the fact that a[k] is not changed.
In summary,
For all k >= l, we need to add v*(l-1) to the correction values
For all k > r, we also need to subtract v*r from the correction values
Since we need range updates and point queries, we use a difference array segment tree to quickly update ranges of c[k] and find any c[k] quickly
So any range update requires us to set c[l] += v*(l-1) and c[r+1] -= v*r. Here c is a difference array segment tree.
Any sum from a[1] to a[k] is just a[k]*k - c[k]
Any range sum from a[l] to a[r] is just the sum from a[l] to a[r] minus the sum from a[1] to a[l-1]
And that’s how you have fast range sums and range updates without using a segment tree!
Moral of the story:
Sometimes, changing the way you represent data in a data structure can be more useful than changing the data structure itself. Like representing data using difference arrays and creating a Fenwick tree to track the difference arrays is a fast solution to find range sums and execute range updates.
Final Challenge
The first reader to submit their solution to this challenge stands a chance to redeem a free PDF from the referral rewards page!
Your challenge is to solve the initial challenge posed in the last article, but with range updates. Using Fenwick trees, create a program in a programming language of your choice that
Accepts user input
Allows me to update ranges of student scores
Allows me to track the total number of students that scored within a specific range of scores
Uses Fenwick trees and difference arrays (not alternative data structures such as segment trees)
In line with attempts to shift towards paid subscriptions, the code for the Fenwick tree’s full implementation is only available to those who have pledged pay to read Elucidate: for the curious coder. If you are one such pledger, text me on the Substack app or website to view the code. If you would like to become a pledger to support my work, you can pledge your support by clicking the button below.
Click below to learn about other ways to support the publication, or why supporting me is important.
To redeem other prizes such as exclusive free PDFs, help by referring this publication to your friends.
Thanks for reading, and I’ll see you in the next one!