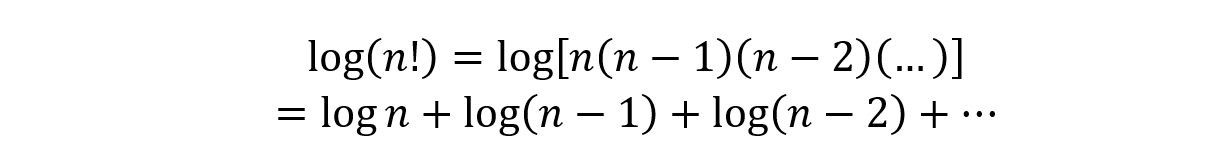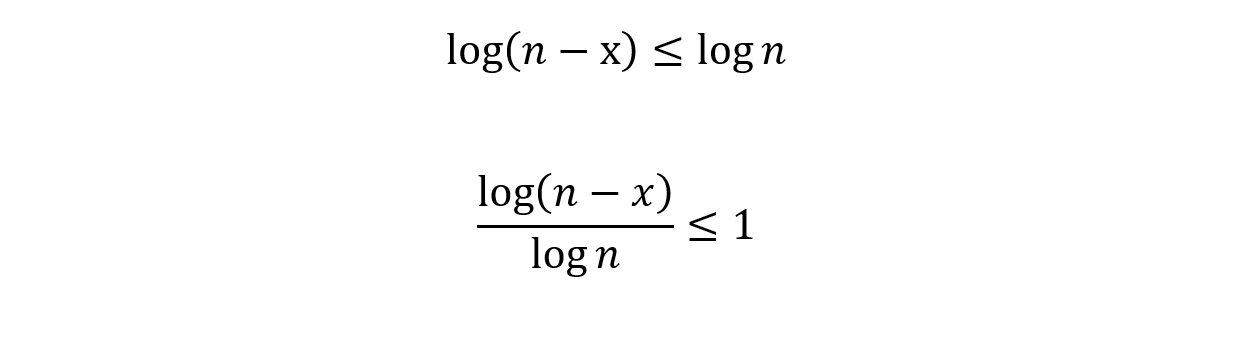A lower bound on sorting
Why we can't have faster sorting algorithms
A fundamental problem in computer science is the problem of sorting some data. Whenever we sort something, we’re making problem solving easier because our data now has a predictable order. For more information on sorting, see this article.
The main problem in sorting is that it takes time. Currently, our fastest sorting algorithms are said to “have a time complexity of O(n log n)”. What does this mean? Well, it’s essentially saying that n log n is an upper bound on the number of steps it takes to sort a list of length n with our best algorithm. But the question remains, can we sort a list faster than this?
The answer is yes, but only for very special cases. If we have a general array, there is no faster way to sort it, and this article explores exactly why. It’s a thrilling mathematical journey with a satisfying proof to conclude it, so enjoy!
Formalising the problem
A lesson learnt from my competitive coding days, before solving any problem we must first get a formal definition. So let’s make some terms clear.
Definitions
A general array is an array where we have no information about the array, but we can compare 2 items and query which is smaller.
This means the array has no special properties, no possible exploits. All we need to know to sort any array anyways is which elements are lesser than which other elements to get an idea of how to order them. That’s what our best algorithm is doing,
The time complexity is a measure of how the number of steps taken by the algorithm scales with the size of its input. We will go through this concept again later in the article
Introducing information theory
Before we start the formal proof, there’s some pre-requisites to cover, one of which is information theory. The actual field of information theory is vast and beautiful, and I highly recommend anyone interested check it out. But for now, an introduction will suffice.
Information comes in units called bits. This isn’t to be confused with the binary digit, which is also called a bit. A bit of information is a term coined to attempt to quantify information. What exactly does information mean?
To start off, let’s say an event x has a probability p(x) of happening. One says,
Woah, let’s break this down, shall we?
p(x) is between 0 and 1. It’s how likely the event is to happen. The logarithm is in base 2, as is the usual case in computer science.
If p(x) = 1, I am certain that the event will happen. Hence I gain 0 bits of information. The event happening does not tell me anything.
If p(x) = 0.5, then it means the event has the same chance of happening and not happening. If the event happens, I say I gain 1 bit of information.
As the probability of x happening reduces, I get more and more information from x happening.
Now, what we’re really concerned with is the 2nd case, where the probability of something happening is 0.5, or 50%.
We can model this case as us being at a crossroads. In front of us there are 2 possibilities, we can either go left (0) or right (1) at each crossroad. So we can model our crossroad as something like this..
We have 4 destinations. Each destination is described by a series of steps required to get there, where 0 means we take a left turn and 1 means we take a right turn. So the destination 00 is reached by 2 left turns, while the destination 10 is reached by a left and then a right turn.
Notice that each step in our decision tree has 2 branches, the equivalent of saying an event has 0.5 probability. Which means we gain 1 bit of information for every step we take. The end of this decision tree has 4 possible states (00, 01, 10, 11). Hence, 2 bits of information give us 4 possible states. And in general, n bits of information give us 2^n possible states. Try expanding the crossroads above to see exactly why this is the case.
You might be wondering what any of this has to do with sorting, but I promise that part is coming soon. First, though, we need to continue going through pre-requisites, so remember what you’ve learned about information theory so far. We’ll need it again later.
Big O notation
This part is only slightly harder to understand, but if you follow along slowly, you’ll get the hang of it.
Before going through this though, we’ll make a few observations.
Observations:
1.A computer can perform on the order of hundreds of millions of operations every second. The exact number of operations depends on the hardware of the system.
2.
Any algorithm is made up of several steps. Hence algorithms take time
3.
We want a way to express how much time an algorithm takes without the exact system specifics mattering very much.
Implication
We only want an upper bound on how many steps an algorithm will need in terms of the input given to it, not the exact number of steps it takes. That’s where big O notation comes in.
Now that we know what exactly big O notation is, let’s formalise it. The formal definition for big O notation looks like this:
Again, WOAH! What does it even mean?? Let’s go through it step-by-step to explain each part of the equation.
Unpacking the maths
Step 1: We want an upper bound on f(x)
Remember, that’s the point of big O notation, an upper bound on the number of steps the algorithm takes. So let’s say the algorithm takes f(x) steps given x inputs. Then we want a function g(x) that can be an upper-bound on f(x).
Where M is some constant. Why a constant? Because the exact number of steps doesn’t matter remember? We just want a rough upper bound. The constant M doesn’t matter because different machines execute code at different speeds.
Step 2: As x increases
This part is somewhat optional, but since it’s in the formal definition, we want to include it. Basically the upper bound may not apply to very small values of x which could be exceptions, which is why we choose some value x0 as the minimum x.
By the way, the double arrow means “implies that”. So if x is greater than our minimum value, then f(x) is bounded by Mg(x).
Step 3: These values should exist
The last part of the maths is trivial. If f(x) = O(g(x)), then M and x0 must both exist.
The weird shaped E just means “there exists”, and the weird looking Z+ just means “in the set of all positive numbers”.
That’s it! That’s all the big O notation means. So in English, we’re just saying “We can have an upper bound on f(x) in terms of g(x) if x is big enough”. That’s it. It’s that simple.
So as a more complete example, say our algorithm takes 2x steps, that is, f(x) = 2x. Then if we let M = 3, then we can show that
Hence 2x = O(x).
Simple? Now let’s start the formal proof
Formal Proof Of the Theorem
Lemma 1: There are N! permutations of an array of n items
Proof:
Imagine we have the task of arranging N items.
There are N ways to choose the first item.
That leaves N-1 ways to choose the second item. And N-2 ways to choose the third item. And so on until all N items are chosen.
So the total number of permutations is N(N-1)(N-2)(…) = N!
As an example, consider an array of 3 items, 1, 2, 3. The permutations are
[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]
There are 3! = 6 permutations of an array of 3 items.
Lemma 2: The best general sorting algorithm will take at least log(n!) steps
Proof:
This is where information theory comes in!
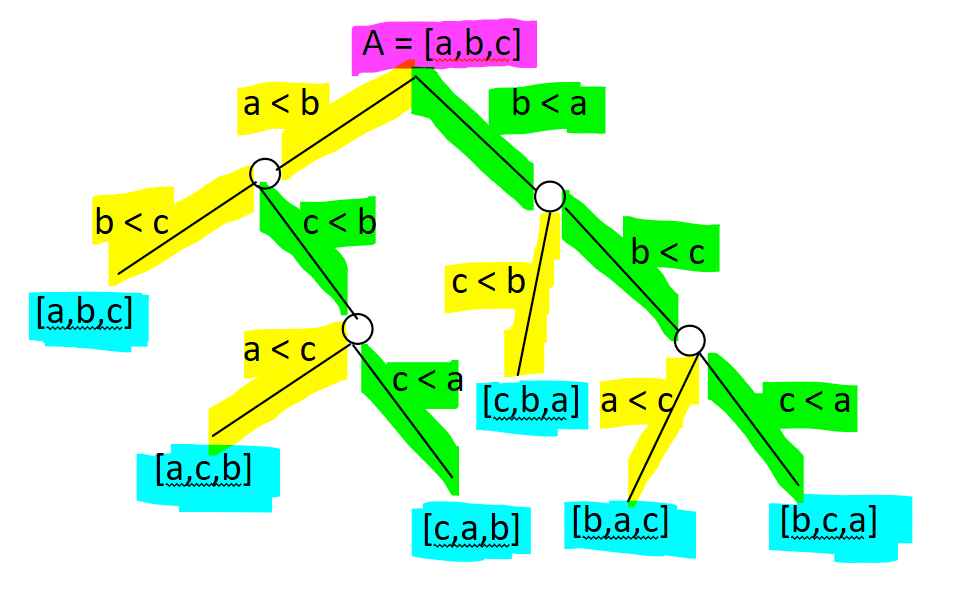
Let’s model our sorting algorithm using the steps we discussed in the introduction to information theory. We know that a general sorting algorithm can only sort by comparing 2 items. So, we can model the algorithm as a series of comparisons. Every comparison takes 2 items and compares them. As a concrete example, consider there being 3 items.
Here, I’ve represented the paths in yellow and green instead of ones and zeroes because it’s more visually intuitive. The destinations are in blue. Notice that the destinations are all different permutations of our array. The best sorting algorithm makes the right comparisons every time and reaches the sorted array as fast as possible. Does this model of paths and destinations sound familiar?
It’s the same as the crossroads we created when learning about information theory! Remember from the information theory section that in general, if we have n bits of information (n steps in the crossroads or decision tree), then we have a total of 2^n possible states.
If we treat every destination as a state, then
There are n! destinations, one for every permutation of the array
The best algorithm takes x steps to find the sorted permutation
An algorithm that takes x steps gains x bits of information. There are a total possible n! states, which is the same as 2^x in the worst case. So,
Therefore the number of steps taken by the best sorting algorithm has a lower bound of log(n!)
The log we use here and throughout this article is in base 2.
Let’s now combine our 2 lemmas into our final theorem.
Theorem: log(n!) = O(n log n)
Proof:
Remember from our definition of big O notation from before, we’re looking for an upper bound on the number of steps this algorithm will need, so let’s again solve this step-by-step.
First, the number of steps in this case is,
We’ve replaced the variable x from the big O notation section with n instead. It’s more consistent with the proof this way.
We’re looking for an upper bound in terms of nlog(n), so
You may notice that the n > n0 is missing, it was there when we discussed big O notation remember? Well, the reason it isn’t here is because we’re going to start by assuming that n is always big enough, and we can find the lower bound on it later.
Okay, now our job is simpler. We want to find M. So let’s re-write the question.
Let’s apply basic logarithm rules. Whenever we have a product inside the logarithm function, we can always split it up into its components like this.
Now, let’s use our above expansion to re-write the inequality that defines our big O notation.
Let’s divide both sides by log(n).
We’re making very good progress and, in fact, are very close to the final solution.
The key observation comes here. Notice that,
For any positive value of x. Therefore, we know that the upper bound of the number of steps we need to take.
We’re so close!
Now, just multiply all the terms by log(n) again to get the final answer!
Does this equation sound familiar? It’s exactly what we wanted to show!
And that concludes the proof with our final statement,
Why n > 1? Because when n < 1, log(n) is negative, so the inequality doesn’t hold anymore. And at n=1 both sides are just 0, it while the inequality does hold it’s not really useful.
But that concludes it! We have successfully proven the lower bound for the performance of a general sorting algorithm!
To summarise…
A general sorting algorithm sorts an array with no knowledge about it except for that gained by comparing 2 items in the array
Big O notation gives a general upper bound on the number of steps taken by an algorithm
Information theory teaches us that log(n!) is the minimum number of bits of information needed to find the sorted permutation of the array, and each step gives one bit of information
If n > 1 then log(n!) < n log n
So we know that the fastest sorting algorithm has a time complexity of O(n log n). This algorithm does exist, it’s called merge sort, and you can check it out here
Isn’t that beautiful!
You made it to the end! Thanks for reading. This was quite a long article, and if you enjoyed it, subscribe to never miss a post and keep up to date with every article!
And do consider sharing this content with other curious coders. After all, it’s hard work writing alone...