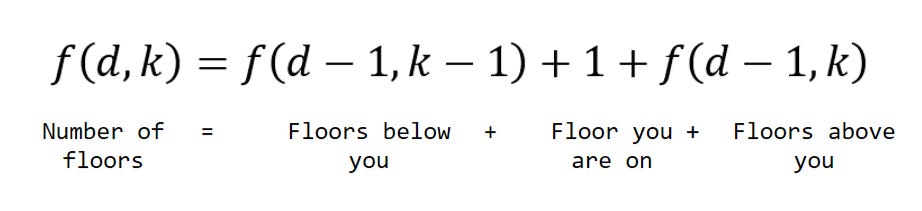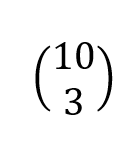The Falling Eggs Puzzle: Part 2

Continuing the dynamic programming adventure

Last week’s problem has been keeping you up at night, because you don’t think you’ve solved it just yet.

Using dynamic programming allowed you to reach a solution. But somewhere inside, you know that you can do better. In fact, there is a much faster solution, but it requires a little bit of thinking out of the box. Today we’re going to explore how to do just that. It turns out, the solution reaches into what initially seems to be a completely unrelated field, until you think about it deeper.

Dear readers,

The long awaited big post is finally here! So big, in fact, that it must be split into 2 parts. Thank you all for your patience and support. These 2 big posts will each have a free section, and a paid section. In order to experience the full thing, and also support my contribution to building up your problem-solving skills, consider becoming a paid subscriber. To those who aren’t already subscribed, consider joining the family for new brain-boosting content every week!

Sit back, relax, and happy reading!

Recap- the initial solution

The initial solution to the problem relied on using a simple, recursive function.

This solution ran in O(KN^2), improved to O(KN) by using monotonicity, as paid subscribers will know.

The Falling Eggs Puzzle: Part 1

But today we need to ditch this function. Why? Well, consider this.

• This function has N*K states by necessity

• Because of the very definition of the function, there cannot be a solution less than O(NK), since all states must be considered

• Therefore, using this function means we are foolishly restricting ourselves to a slow solution.

Can you find the fast solution before reading further?

Re-imagining the problem

First, it is necessary that we completely forget the existing definition of the function f. Instead, it’s time to focus on creating a new problem-solving view point.

To do this, we turn to an age-old favourite tool- binary search! Of course, it needs to be used from a perspective we aren’t used to. Recall what the question asks…

what is the minimum number of drops I need so that I am guaranteed to solve the problem

We are, indeed, going to binary search the minimum number of egg drops needed. Paid subscribers will know that previously, we used binary search to directly search for the answer to the problem by computing f(n,k) faster. But this time, binary search needs to be used differently. Let’s see how.

A new function

Let’s re-write the function f in words first.

Suppose we restrict ourselves to d drops of k eggs. Then let the function f(d,k) be the height of the tallest building such that I can always obtain a solution within d drops of k eggs. Notice that the more drops I have, the taller the building that I can test, so f(d,k) is monotonically increasing with respect to d. Now we need to use binary search on d.

• For any value of d, if f(d,k) < N, then the building is too tall. Guess a larger value of d.

• Otherwise, if f(d,k) > N, then we have enough drops, and therefore can try smaller values of d to see if a more optimal solution exists.

• Binary search finds the smallest d such that f(d,k) >= N.

Defining f

As usual, we use the definition of f(d,k) in words to construct a mathematical definition.

• Suppose for some d and k I let f(d,k) = N.

• This means the tallest building I can possibly test with d drops of k eggs is N floors tall

• Picture yourself standing on any floor of this building. The egg can either break, or not break.

• Imagine you drop the egg and it breaks. You will now use d-1 drops of k-1 eggs to test all the levels below the one you are on now. But remember that since we want to find the tallest possible building, the number of floors below you must also be as large as possible. So below you, there are f(d-1, k-1) floors

• Similarly, if the egg does not break, you will now use d-1 drops of k eggs to test all the levels above the one you are standing on. Again, the number of levels above you must be as large as possible, so above you there are f(d-1, k) levels.

• We have a mathematical formula now.

You may be wondering why the level we drop the egg from doesn’t matter. That’s because since the height is maximum, we assume that you use all your drops optimally. So you must have dropped the egg from the best possible level. Remember how at first we needed to search for the optimal level in the old solution? Now, we simply start by assuming you already know the optimal level.

If we binary search the answer using this function, the solution has a time complexity of O(NKlogN). Why? Well, there are N*K states we need to compute for all values of f(d,k). Logically, we won’t need more than N drops to test a building N storeys high. Therefore, max(d) = N, and there are N*K states. Since we binary search all values of d from 0 to N to find the smallest d such that f(d,k) >= N, the total time complexity is O(NKlogN).

To most of you, this is a significant improvement from the O(KN^2) we stopped at last time. But for the paid subscribers, we obtained an O(NK) solution, so this is actually worse. Until, we find out that this is not the complete solution. Here’s where the surprise comes in.

Combinatorics in problem solving

Let’s learn a new mathematics chapter- combinatorics. Have you seen this notation before?

That’s pronounced “n choose k”. It’s the number of ways of choosing k objects from a total of n. For example, if there are 10 students in a class, the number of ways that you can choose 3 students is 10 choose 3, written like this.

There’s a formula for this, whose derivation is also pretty simple.

We then account for repetition. For example, when choosing 3 objects, the choice (1, 2, 3) and (2, 3, 1) are the same choice.

But how on earth will this help us solve our problem?