The Big O
Time complexity analysis
Today we’ll learn about time complexity analysis. It is a useful tool to analyse algorithms we design, and is crucial to all competitive coding tasks.
What is it?
Big O notation is a way to tell how much time an algorithm will take depending on how big its input is. Remember, an algorithm is a series of steps we define to solve some problem. In competitive coding, an important factor apart from the algorithm being correct is it being fast, and that’s what we’re interested to find out about with this technique.
How is it implemented?
Let’s start of showing how it looks like. We say that an algorithm has time complexity O of something. We write it using the letter O as a function. For example, if we say an algorithm has time complexity O of n, we write it the time complexity as
This case is also called linear time complexity. Here’s another example. If we say an algorithm has time complexity O of n squared, we write it as,
Simple enough? Now let’s get to the bottom of what this means exactly.
What does the function mean?
It would be more beneficial instead of directly defining the function to give some examples of various time complexities and how to find them.
First, let’s start a simple one. Let’s say our algorithm has only one step: it adds 2 numbers together. Let’s call them a and b. On a computer, adding computers is a single operation that takes negligible time, so we call this a constant time operation. In other words, the time taken does not change significantly as the inputs, in this case a and b, change.
Now another example. Suppose we want to add n numbers together. In the previous example, there were exactly 2 numbers every time. But now, there are n numbers, where n is some variable we specify to the function. Remember that adding 2 numbers has a time complexity of O(1), when we add n numbers, we say we have linear time complexity.
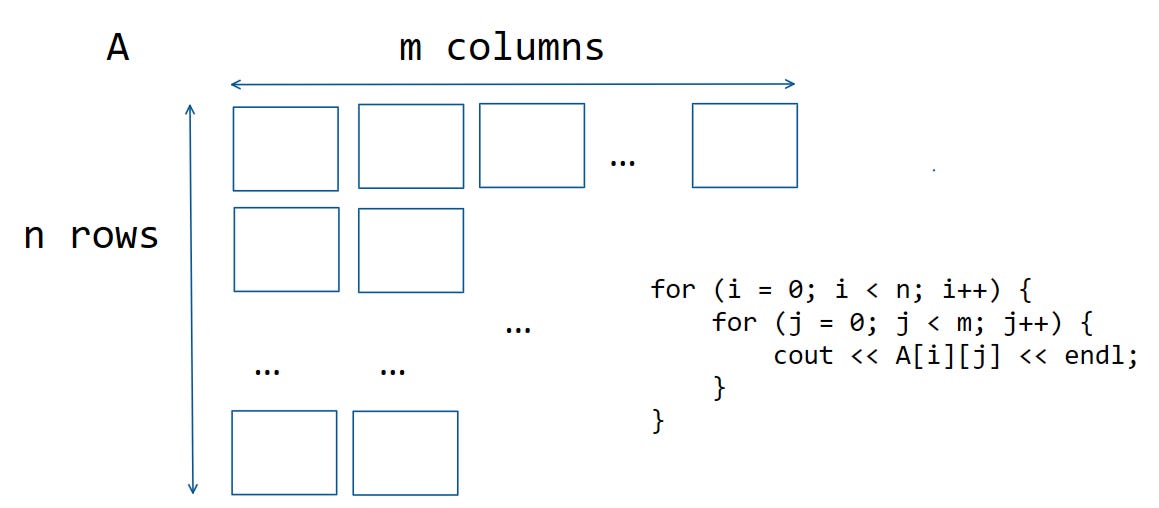
I think you can see the general idea now. Let’s have another example. Suppose we’re looping through a matrix A that has n rows and m columns.
It’s basic maths that there are n*m total items in this matrix, so the total time complexity here is O(nm).
Great, by now you should be able to see the general pattern. Big O notation is a way of understanding the approximate number of steps that an algorithm will take.
General rules for big O notation
When finding the time complexity of some algorithm, remember the following rules.
Constant time operations don’t count
If some step in the algorithm is repeated the same number of times every time the algorithm is run, it doesn’t count in the time complexity of the algorithm.
For example, say our algorithm prints ten words, or adds 7 numbers together, or multiplies 3 decimals, and so on. These steps all have time complexity of O(1).
This means that constant terms in the analysis must cancel out. So if you find that your algorithm has time complexity O(2N), for example, that’s the same as saying it has time complexity O(N).
Add independent operations together
This one’s easy. If you’re algorithm has one for loop with time complexity O(n), and another with time complexity O(m), then we add them together and get time complexity O(n+m).
for (int i=0; i<n; i++) cout << "This has time complexity O(n)" << endl;
for (int i=0; i<m; i++) cout << "This has time complexity O(m)" << endl;
// total time complexity O(n + m)Multiply nested loops
This should also make sense. If there are nested for loops, one with time complexity O(n) and another with O(m), the time complexity is O(nm). Think about why this happens…. I’m repeating an O(m) operation n times.
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
cout << "Time complexity: O(nm)" << endl;
}
}Use the largest exponent
This one is more important in the future, but just remember this simple rule. If the time complexity is polynomial, then only consider the term that has the highest power.
This rule seems abstract but, trust me, you’ll see it come into play later.
How fast exactly is a fast algorithm?
This is the critical question. A typical computer can perform on the order of hundreds of millions of operations per second. So the function is good if the number of operations needed is less than a hundred million in the big O notation.
For example, suppose we want to find the largest number in a list of n numbers. Looping through this entire list to find the largest is our algorithm. Since it has n steps, the time complexity is O(n). So it will be fast if n is less than 100 million.
Similarly, if we have an algorithm of time complexity O(n^2), then it is fast if n is less than ten thousand.
So there we have it, that’s how you tell if an algorithm is fast.
How can I visualise this?
There’s a diagram used to see how quickly different algorithms scale with input sizes depending on the big O notation. It shows some common time complexities and how fast the number of steps increases.
Above you’ll see the most common time complexities, listed below.
O(n!)
Factorial time complexity.
Good for n < 11
Example: There are n! permutations of n unique objects, an algorithm that loops through all of them has complexity O(n!)
O(2^n)
Exponential time complexity.
Good for n < 26
Example: There are 2^n total subsets of n unique objects, an algorithm that loops through all of them has complexity O(2^n)
O(n^2)
Polynomial/Quadratic time complexity.
Good for n < 10K
Example: In an array of n items, the total number of ranges defined as (start index, end index) is n(n-1) = n^2 - n. Using the time complexity rules from before this is O(n^2).
O(n log n)
Logarithmic time complexity
Good for n < 4.5M
This is the fastest way to sort an array of n integers. We’ll discuss this again in a future article.
O(n)
Linear time complexity.
Good for n < 100M
Example: looping through an array of n items to find the maximum item has time complexity O(n).
O(log n)
Logarithmic time complexity
Very good, scales very slowly so n doesn’t matter that much.
Example: Searching for an item in a sorted array of n items.
Note: the log used here is in base 2, because computer scientists often use base 2 instead of base 10. But because of the rules of big O notation, the base doesn’t really matter, see if you can derive why.
O(1)
Constant time.
Usually this is not possible except in very idealistic scenarios.
Examples include addition, getting an item from an array, and other simple built-in operations.
We’ll see examples of the above time complexities in algorithms in different articles.
Is there a more formal definition?
Yes, but this one’s more for the math nerds, so skip this part if you don’t really get it.
In other words, we can establish an upper bound on f(x) in terms of g(x).
For more detail you can check out the Wikipedia page. This above definition helps explain the rules of analysing time complexity and I do recommend that you check it out if you understand the math behind it.
Thanks so much for reading! Subscribing is a constant time operation that gives me exponential happiness, so please consider joining the community here at Elucidate.
And if you’re already here, why not share it with your friends if you’re sure they’ll enjoy this content too? The more the merrier!