Solving Coin Puzzles
Unique ways to use binary search
Today’s puzzle has sent you to the royal palace of a land far far away
The king has placed stacks of coins in front of you. There are a hundred thousand stacks of coins. A coin weighs exactly one kg, except for a single fake coin that actually weights 2kg! But the king is a busy man, so he has limited you to ask no more than 30 questions. In each question, you get to select some stacks, and the king’s men will tell you the weight of all the stacks you chose to measure. Within 30 measurements, he wants you to find which stack contains the fake coin. How do you answer his question?
You’ve got to think smart to solve the king’s problem.
Your brain is a muscle that must be regularly exercised. Subscribe to get weekly brain workouts through interesting problems like this one.
If you’re a regular here, you can trust that I deliver quality work with every article. All I ask is less than 2 cups of coffee a month as encouragement.
Binary Search
This problem (using stones instead of coins) was posted in Algorithmically Speaking. Thanks to Alberto Gonzalez Rosales for the collaboration!
This article is the solution to his challenge problem. If you’re unfamiliar with binary search, you should give that article a read first.
Understanding the problem
You know you have an array, a. a[i] is the number of coins in the i-th stack of coins. If we start with the naïve solution, then we can ask the king the weight of every single stack. The i-th stack should have a weight of a[i] kg, since every coin weighs 1kg. But in the stack with the fake coin, the weight of the stack should be a[i]+1 kg, because the fake coin is 1kg heavier than the rest!
But if you check the weight of every single stack, you need to ask 100 000 questions to the king! Besides, the king could have just measured the stacks himself. Why would he call you here otherwise? He wants you to save his time by working within the 30 question limit.
The clue hidden in the task
The clue is that you don’t need to measure the stacks one-at-a-time. The king has allowed you to measure the weight of multiple stacks at the same time. So let us create another array, w. w is called a prefix-sum table. It stores the sum of all numbers in hte array a from a[0] to a[i].
w[i] = a[0] + a[1] + ... + a[i]
// shortcut to code above:
w[0] = a[0];
for (int i=1; i<n; i++) w[i] = w[i-1] + a[i]Let’s assume that there is no fake coin. Then if we weigh the first i stacks, their weight should be w[i].
But if one of the stacks among those we selected to measure is fake, then their weight must be w[i]+1!
Creating the predicate
If you’ve read Alberto Gonzalez Rosales’ post I linked earlier, you’ll know what a predicate is. Otherwise, here’s a quick summary. A predicate is a question we ask whose answer is either true or false. Given an array, we imagine asking this predicate to every element in the array and checking the answer. The predicate must be designed such that it divides the array into exactly 2 halves- one where the answer is always true and another where the answer is always false. In this case, the predicate we ask each element is,
Is the weight of all the stacks until this stack equal to the number of coins? In other words, is
w[i]= the weight of all stacks of coins from 1 toi?
This is true for all values of i before the stack with the fake coin. If you don’t understand this part, don’t worry. Maybe it will help if we illustrate the solution.
Illustrating binary search
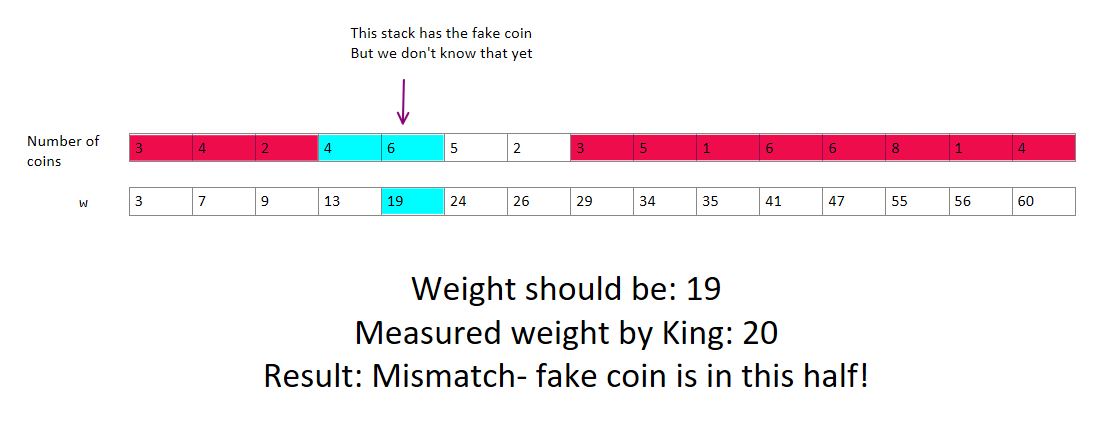
First, let’s create our stacks of coins. Suppose that there are 15 stacks. w[i] stores what the weight of the first i stacks should be if none of them are fake.
Binary search slowly narrows down the range we need to check. To start off, we can guess that the fake coin is in the first half stacks.
We found the coin in the first half, so we can eliminate the entire second half of the array, since we know the fake coin is not there. Let’s highlight that eliminated range red. Within our narrowed down range, we again guess that the fake coin stack is somewhere in the first half.
Now we have narrowed down our range even further. We highlight these stacks red. We’ll continue using them in our measurements, but we can be sure that they are not fake. Again, guess the midpoint of the narrowed down range.
The range is now super narrow! There’s only one thing left to check- which of our last 2 narrowed down stacks is fake? As usual, we assume the first half.
And now we should have our solution!
Time complexity analysis
Binary search has a time complexity that’s easy to analyse.
In every iteration, we halve the size of the search space.
If there are n items in the search space, we need no more than log(n) steps to find the correct item.
Hence, binary search is said to have a time complexity of O(log(n)). The logarithm is in base 2. And lucky for you,
log(100000) = 17 (rounded up)
So you’ll be able to solve the King’s problem and still have 12 questions left over!
Of course it’s not that simple
You didn’t think the King would let you off so easy now, did you?
You’d have thought the King would be happy with your solution, but he’s in a bloodthirsty mood today and is very angry that his perplexing problem did not confuse you enough. He has gathered all the stacks of coins (replacing the fake stack with a real one) and now, there are 100 000 stacks of coins laid in a line in front of you. Here’s your new task.
The King presents 100 boxes in front of you. He has labelled the stacks of coins from 1 to 100 000. You need to place the stacks into the 100 boxes according to the following rules.
Every box must contain at least one stack. You do not necessarily need to distribute the stacks evenly among the 100 boxes.
Every box must contain a consecutive subsegment of stacks. For example, the first box contains stacks numbered 1, 2, 3, and so on until, let’s say x. Then the next box contains stacks x+1, x+2, x+3, and so on. Basically, the labels of the stacks in each box should be consecutive numbers.
The total number of coins in each box is the sum of the number of coins in each stack in that box. Let M be the number of coins in the box with the most coins. Your aim is to minimise the value of M.
You get up to 30 tries to divide the stacks. By the end of these 30 tries, the stacks of coins must be distributed such that, no matter how else you distribute them, the value of M cannot be reduced any further under the same problem constraints.
In other words, find the smallest value of M such that every box contains no more than M coins, and all the stacks of coins are packed into 5 boxes.
It’s your head on the line this time. What’s the fastest way to solve this problem?
Before continuing, I know you’re excited, but as a reward for providing regular stimulating problems for everyone, all I ask is less than 2 cups of coffee a month. Care to help?
Thinking about the solution
At first, it seems very hard to even get started. There are countlessly many ways to distribute 100 000 coins among 100 boxes. And you can only try 30 of these distributions before the King gets fed up and beheads you. The chance of you succeeding is negligible- unless you’re clever.
It would be easier to think of a smaller problem. Previously, this was done to illustrate how binary search works using just 15 stacks of coins. Let’s return to those 15 stacks, and say we need to distribute them among 5 boxes.
There are over 2000 ways we can pack these stacks of coins, and we really have no time to go through everything, so let’s skip to the smart way- binary search! (again)
Something funny about M
Recall that M refers to the number of coins in the box with the most coins. Since every box must have at least one coin, the minimum possible value of M is 1. If we pack all the stacks of coins into 1 box, we get the maximum value of M. In this case, that value is 60 (the total number of coins in all the 15 stacks).
What if we guess some answer for M, can we check if our guess is correct? Turns out, we can.
If we guess a value of M, we start packing stacks 1, 2, 3, and so on into the first box. Once we can no longer add a stack without exceeding M coins in the 1st box, we move on to the second box and repeat the process.
At the end, if M is too small, then there will be some stacks of coins left over since we can’t fit all the coins into the boxes.
Otherwise, all the coins will fit. We want to find the smallest M such that all stacks of coins will fit into the stack
This leads nicely on to our general rule of binary search.
We can use binary search to solve minimisation or maximisation problems by guessing and checking the answer
Let’s explore how it works.
Binary search on M
In our case, we know that M is between 1 and 60. So let’s guess M = 30.
Is that big enough? Let’s see. Starting from the first box, we pack as many stacks as possible into it without exceeding 30 coins in total.
We start of by putting stacks 1, 2, and so on into the first box. In the end, we put 3 + 4 + 2 + 4 + … = 29 coins into the first box (these stacks are highlighted yellow). The next stack has 5 coins, and 29 + 5 > 30, so we have to move on to the next box. We repeat the process, at the end of which the second box has 27 coins. The last stack has 4 coins. 27 + 4 = 31, which would exceed our limit, so we put the last stack in a box of its own. In total, we need only 3 boxes for M = 30. Therefore, M must be smaller than 30. Let’s now guess M = 15.
We need more boxes this time, but it still works. No box has more than 15 coins, and all the stacks of coins still fit. Now we know that M should be between 1 and 15. Guess 8 as the mid point.
Off by a long shot! If we restrict each box to contain no more than 8 coins in total, we’ll never pack all the coins into the boxes! M must be somewhere between 9 and 15. Guess M=12.
So close, but not quite enough. If 12 is not enough, we now know that M is between 13 and 15. So what do we guess? 14!
Turns out M = 14 is enough. The only number we haven’t tested yet is M = 13. But it turns out, none of the boxes in the above have more than 13 coins (check it out yourself), therefore our final answer is M = 13!
General solution
We binary search the value of M. Even if there are more than a thousand coins per stack (which there probably aren’t), you’ll be able to get this within 30 guesses. In each try, guess a value of M, and see if it works. Once you answer the king’s problem within 30 attempts, he is pleased and forgives you.
He tried his best to outsmart you, but alas, curious coders just can’t be beaten. Impressed by your intellectual prowess, he lets you go off and reflect on what you’ve learnt.
Reflection
This exploration has given you insights into new ways to use binary search that you may not have already known. Some things you can learn are,
Binary search can in general be used for minimisation or maximisation problems
You can guess and check the answer to a question, working backwards till you find the right solution
Considering smaller cases of a problem can often yield insights than can bring you to a general solution
Binary search really is one of computer science’s most amazing algorithms, with wide ranging applications you never even knew were a thing.
Thanks for reading, and I’ll see you in the next one!
Please consider supporting my work if you enjoy these problem-solving adventures. All I ask is less than 2 cups of coffee a month. In return, you enjoy consistent brain-boosting problem-solving articles, without fail, every single week.
Final questions before you leave, please comment your responses below.
Did you enjoy this read?
Why is binary search so much faster than normal search? Is there something you can take away from this?
Can you think of other use cases for binary search?
Did you know that there is another kind of search with the same inspiration called ternary search. Can you find an application of it?
Finally, can you code a solution, in any programming language, to one of the problems above and send it to me to redeem a free prize?
Eager to hear from you.
See you in the next one!