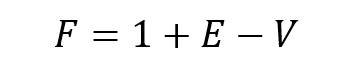Today’s problem involves you drawing circles on a piece of paper one boring, rainy Sunday evening.
The question you pose is simple.
Draw N points on the circumference of the circle.
Connect every point to every other point by a straight line
Ensure that every intersection in the circle must be one of exactly 2 lines. If 3 or more lines intersect at the same point, re-start.
Once you are done with this process, how many regions have you cut the circle into?
Dear reader,
Thank you for supporting Elucidate: for the curious coder. These next few weeks are going to be busy, so expect the length of articles to reduce for a short while.
It’s hard work writing alone. I appreciate all support for my writing. Please consider pledging your financial support- I ask for less than 2 cups of coffee a month, and in return you get a new brain-boosting problem solving adventure every week.
Subscribe or pledge your support here
At the end of these few weeks, I’ll release a much longer article that will be an enjoyable read. Till then, all help is much appreciated.
Solving the problem
There’s a cool pattern you’ll notice.
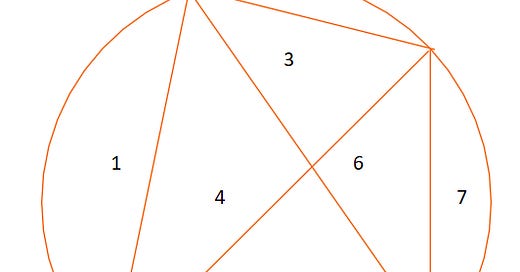
When N = 2, you draw a single straight line in the circle. You cut it into 2 regions.
When N = 3, you draw a triangle in the circle, cutting it into 4 regions.
When N = 4, you cut it into 8 regions.
When N = 5, you cut it into 16 regions.
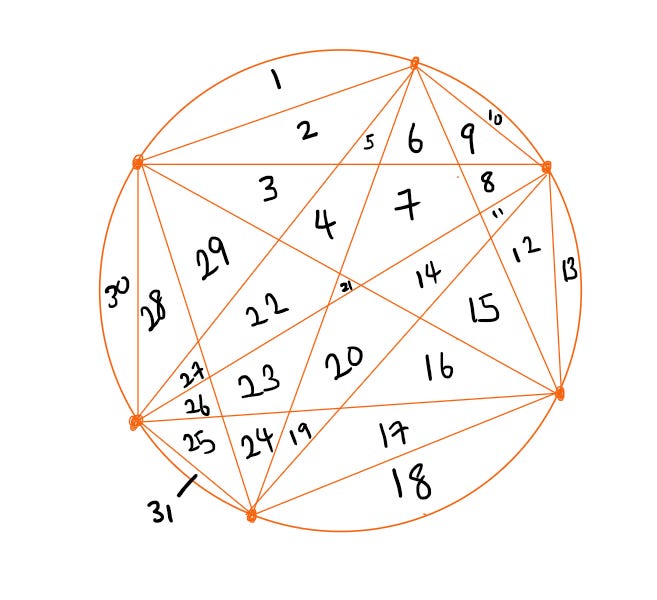
It seems like a simple pattern. Just consecutive powers of 2, right? So, what happens when N = 6?
Just shy! It’s only 31 parts. So, what happened?
Euler’s formula
At first, though this may not look like it, this is a graphical problem, not just a geometrical problem. Solving it involves a mathematical trick that we can use. And this is Euler’s formula.
First, we need to define a planar graph.
A planar graph is one where none of the edges intersect one another when the graph is laid out on a 2-d plane.
Now let’s create 3 variables to represent a planar graph.
Let V be the number of vertices in the graph
Let E be the number of edges in the graph
Let F be the number of regions in the graph
We can make 2 important observations about planar graphs.
Think about what happens when you add another edge to a planar graph.
If you add an edge to a planar graph that connects an existing vertex to another existing vertex then the number of edges increases by one, as does the number of regions in the graph. Since both E and F increase by 1, F-E remains a constant.
If you add an edge to a planar graph that connects an existing vertex to a new vertex, the number of vertices increases by 1. The number of edges also increases by 1. The number of regions you have created does not change. Since both V and E increase by 1, V-E remains constant.
Consider now the expression V + F - E. If you increase V by 1, you increase E by 1. If you increase F by 1, you increase E by 1. So the V+F-E remains unchanged.
Since this value is a constant for all planar graphs, we can use the above graph as an an example.
V = 4
E = 4
F = 1
V+F-E = 4 + 1 - 4 = 1
This gives us an important equation to work with from now on.
In the final graph, we want to find F. So, we can re-write this equation.
Now we need to find V and E in our circle.
Number of vertices
In order to treat our circle as a planar graph, we need to treat every intersection between 2 lines as a vertex of its own. That way, we know no edges intersect, and the graph is planar.
Now, we need to make a claim and prove it.
Claim: For any set of 4 points on the circumference of the circle, they have exactly 1 intersection, and that intersection is unique.
Proof:
Consider some 4 points.
If we draw every possible line connecting 2 of these 4 points, exactly 2 of these lines will ever intersect (the 2 diagonals). And since no point is the intersection of more than 2 lines, as defined in the problem statement, any 4 pairs of points has a unique intersection in the circle. That ends the proof.
Therefore, the number of vertices in the circle is equal to the N vertices on the circumference plus every intersection between 2 lines. Since every point is connected to every other point, the number of intersections is the number of sets of 4 points. How do we do this?
There are N options to choose the first point
Once chosen, there are N-1 options to choose the second point
Then, there are N-2 options to choose the third point
Finally, there are N-4 options to choose the fourth point
However, these 4 points can be arranged in 4! different ways. All these permutations are different ways of writing the same points (e.g. [1,2,3,4] and [1,4,2,3]). Therefore, we need to divide the final answer by 4!.
Let’s write this mathematically.
NC4 is a shorthand that stands for “N choose 4”. It’s the number of ways to choose 4 points out of N.
Number of edges
This is actually quite simple.
Similarly to before, we can find the number of edges using N choose 2 instead of N choose 4. This is because any 2 pairs of points on the circumference form 1 line, or one edge. But that alone is not enough, since we haven’t considered intersections.
Every time 2 lines intersect, we turn that intersection into a vertex. Therefore, from 2 edges before, we now have 4 edges. That means we added 2 to the total number of edges. Notice that for every intersection that is converted to a vertex, we add 2 edges to the total.
We already know from before that there are NC4 edges. Therefore, we add a total 2(NC4) edges.
Number of regions
We’re almost done. Notice that our current graph does not consider the outer parts of the circle.
There are N regions not counted in the graph. Therefore, we need to add N to the final answer.
Now just put in the values already calculated!
And that’s the answer!
Reflection questions
Comment below,
What did you learn from this problem?
Euler’s equation also explains one of the definitions of a tree. Can you spot why? Hint: A tree has 0 regions
Why is this pattern so unreliable?
Thanks for reading, and I’ll see you in the next one.
This article was inspired by 3Blue1Brown’s video on the topic.
If you enjoyed this article, click here to pledge your support. I ask less than 2 cups of coffee a month, and all help is much appreciated.