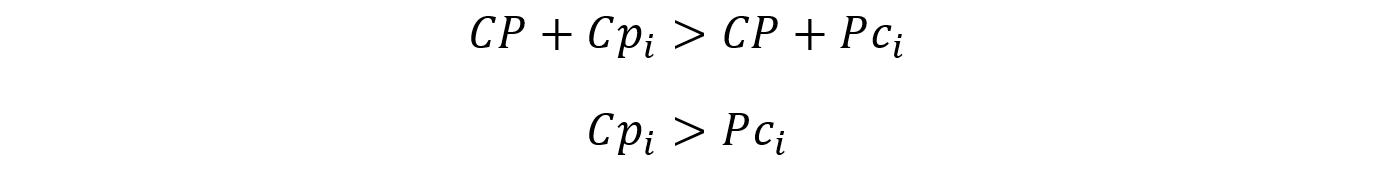Greedy Algorithms
Why fast shortcuts sometimes solve hard problems
But of course you can have your cake and eat it, too – if you decide to bake a second cake. And you may well find that baking two cakes does not take twice the work of baking one.
- Robert Kuttner, American Journalist This article discusses a new kind of algorithm. In previous articles we’ve been discussing more direct kinds, like how to sort a list. But this here is a whole category of algorithms, one that once you learn, will open a new realm of problem solving and a new kind of intuition you didn’t even know you had!
In this exploration, we’ll deep dive into the world of greedy algorithms. We’ll understand what they are, why they exist, how to prove their optimality (yes, that’s a crucial step!) and how to develop greedy intuition. Sit back, relax, and enjoy the read!
What is a greedy algorithm?
Like many things in computer science, it’s exactly what it sounds like. But of course, formal definitions are still important (ugh, right?). So, here it is.
Definition
A greedy algorithm is an algorithm that, in every step of the heuristic problem-solving process, makes the locally optimal choice to arrive at a solution.
Let’s picture what that actually means… What is greedy in English? Think about little kids playing with toys. That one kid who always wants more toys? He’s greedy. At every step of his thought process, he always makes the locally optimal choice, which is to want more toys. In his mind, more is better. Think about someone who always takes the largest pizza slice, or always buys the cheapest item on sale. These are all greedy behaviours. Notice something in common- greediness means always doing what you think gives you the most gain every single time.
An algorithmic example
Imagine a thief has just broken into a bank that stores gold bars. Now, this thief, let’s call him Joe, has k bags to put the gold bars in. The problem- there’s thousands of bars, and each bag can only hold one! But Joe has a special power: he can look at any gold bar, and instantly determine its price! So, if you were Joe, what strategy would you employ to make the most of this opportunity?
The answer is quite obvious- the greedy choice! For every bag, he should always fill it with the most valuable gold bar he hasn’t already taken. By the time Joe’s done, he’s got the top k most valuable gold bars in his possession, a wildly successful heist!
In fact, there’s actually a mathematical proof that Joe’s method is the most optimal one, that is to say there’s no better way he could have chosen gold bars to get more value under the imposed restrictions. I leave the proof as an exercise to the reader. As a hint, use the exchange argument described below. But beyond this, here are 3 example problems that take you through an entertaining journey of why greedy algorithms work, and some places they don’t…
Example 1: Lunchbox
This problem is taken from Singapore’s National Olympiad in Informatics 2016. The problem is titled Lunchbox.
You have to distribute N lunchboxes among M schools. Suppose that school i asks for k[i] lunchboxes. You have a rule saying you will either give 0 or k[i] lunchboxes to every school. What is the most number of schools you can give lunchboxes to?
For example, suppose
N=10, M=4,
k = [3,9,4,2]
The answer is 3, you give it to schools 0, 2, 3.
k[0] + k[2] + k[3] = 3 + 4 + 2 < 10
It is not possible to give more than 3 schools lunchboxes.
What is the best way to solve it? Should we check through every combination of lunchboxes? Too slow. Think about the solution before reading further.
Claim:
The greedy solution, which is to always choose the schools with the least demand for lunchboxes, is always the answer.
Proof (by exchange argument):
Let S be the optimal set of schools I should give lunchboxes to. Let T be the set of schools generated by our proposed algorithm. If S = T, we are done. Otherwise,
Hence, we can always replace the element k[j] in S with k[i], because this will always leave us with extra lunchboxes. And by repeating this process, we can always reach T from S by exchanging elements, without reducing the number of schools we give lunchboxes to!
This kind of proof is called the exchange argument, and follows a simple, rigorous procedure.
Let S be the actual solution and T be our proposed solution
If we can always replace some element with S with some element in T without changing the optimality, then we can change S into T without ever getting less optimal than the solution.
Hence, T is not less optimal than S, so T is also a valid solution.
Alternative proof (by common sense)
Fewer lunchboxes asked for = more lunchboxes left to give.
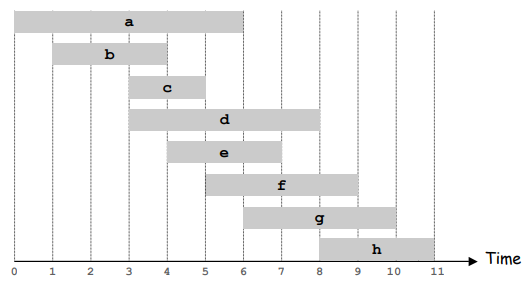
Example 2: Interval Scheduling
This is a harder problem. The source is here. An interesting fact about this particular problem, it seems like a greedy solution will work, but the problem is more nuanced than that…
We have N intervals in an array A. Interval A[i] is defined by 2 values. A start time S[i], and an end time E[i]. Each interval describes a painting job you need to complete.
You can only do one job at a time. So you need to choose some intervals so that none of these intervals intersect. What is the maximum number of intervals you can choose?
There are not 2,not 3, but 4 different possible greedy solutions, only one of which is correct!
Always choose the untaken task that starts earliest
Always choose the untaken task that ends earliest
Always choose the untaken task that takes the least time
Always choose the untaken task that overlaps with the least other tasks
Which of the above is the correct solution? Think for a bit… refer to the example below to see which algorithm works best and see if you can prove it yourself before scrolling down.
Claim
The 2nd method, always choosing the task with the earliest ending
Demonstration
Let’s look at how all 4 methods work on the above example.
The chosen tasks by each algorithm are highlighted. Notice, only methods 2 and 4 give the correct answer: we cannot choose more than 3 non-overlapping tasks to do. But method 4 does not actually work, and here’s a counter-example.
There is no counterexample for method 2. But why? Can you prove it before reading further?
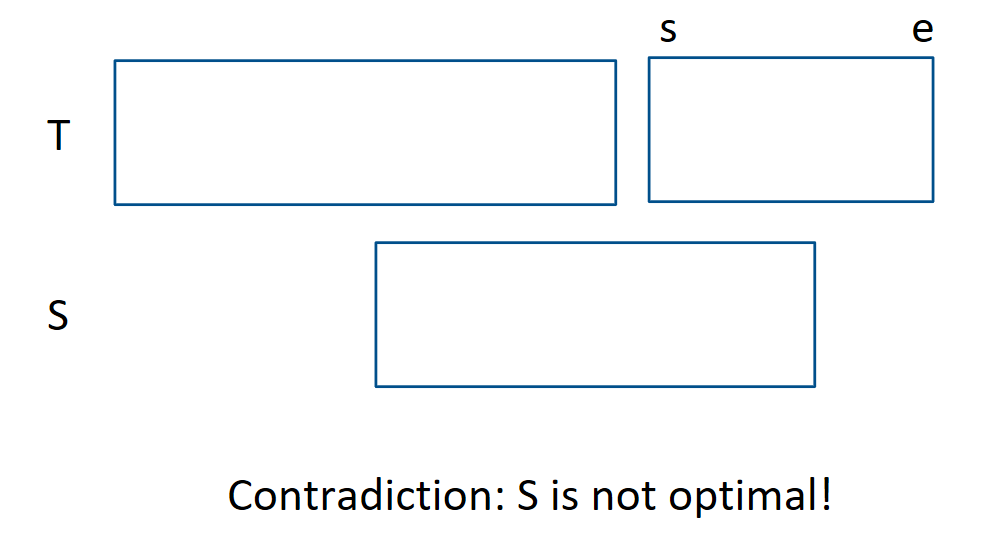
Proof (by contradiction)
Let S be the set of tasks that is the optimal solution to this problem. Now let T be the set of tasks chosen by some algorithm of ours. If S = T then obviously, we are done so we assume this is not so.
How can we use the exchange argument to make S=T without compromising the optimality of the solution in any step?
Choose any task (s,e) in T. Now look at all tasks in S that have an ending time between s and e. Since our algorithm always picks the task with the earliest end time, there must be a contradiction in all cases except for tasks that start before s which we couldn’t take due to overlap. Since all such tasks overlap (their ending times are between s and e and all start before s), we can only take at most one such task by choosing not to take the previous task. However, since this requires replacing 2 jobs with one, it is not optimal and that is a contradiction.
Extending the above argument to the rest of the set, we show that our algorithm must produce the optimal result!
Alternative Proof (by trial and error)
If you run through enough examples, you’ll eventually find that this method is the only one in which you cannot find a counterexample, so it must be correct.
Example 3: Investing problem
This is the last problem we’ll go through. But it’s an interesting one nevertheless. Here’s the problem, taken from this Kattis problem.
You are given N investment opportunities. Opportunity i will cost c[i] dollars to buy, and will earn you p[i] dollars every day. c[i] and p[i] are both always positive. You can buy each opportunity exactly once, but can choose as many of the N opportunities to buy as you want. Find the smallest number of days it will take to earn you M dollars.
For example, suppose N = 2, M = 6, p = [4,10], c = [10,5]
This may not sound greedy at first, but it is! You’ll find, however, that 2 opposing factors, cost and profit, cannot be greedily optimised at the same time, right?
They can.
Claim:
Sort the investment opportunities by c[i] divided by p[i] in some array A. Then there always exists some opportunity, A[S], that we must find, so that the optimal selection of opportunities is all opportunities from A[0] to A[S].
Proof (by induction):
Let’s assume we have chosen some set of opportunities so far, and they have a total cost of C and a total payoff of P. For now, we’re going to ignore the required earning of M, but we’ll come back to it in a clever manner later.
Anyway, notice that it is only good to take an opportunity if it improves the number of days we can make our money back in. Otherwise, we can always just not take that opportunity. So, we can write this mathematically. Suppose that it is optimal to take some opportunity with cost c[i] and daily profit p[i]. Then,
Let’s cross multiply.
Expand the equation.
Finally, we get this.
This means we should only take an opportunity if the payoff time from that single choice is slower than that of all the opportunities we’ve taken so far. Now, here’s the inductive part.
Consider 2 opportunities, i and j. They have cost c[i] and c[i] and profits p[i] and p[j] respectively.
Therefore, on our sorted array A, suppose that we choose to take some opportunity A[S]. Then it is also optimal to take A[S-1] because of how we’ve sorted it. And if we take A[S-1] we should also take A[S-2]. And so on until we’ve taken everything from A[0] to A[S] and hence, we only need to find the best such S.
So the algorithm goes:
For every S, assume we take opportunity A[S]
Find how optimal it is to take all opportunities from A[0] to A[S]
Find the best such S, that’s the answer
Finally, remember at the beginning of our proof we said to ignore the fact that we need to make M dollars in profit, but the above only helps us to make our money back with 0 profit? Well, just add an investment opportunity we must always take, with cost M and profit 0!
Alternative Proof (By intuition):
This is left as an exercise to the reader :)
Intuition in greedy problems
As you have seen, you need a bit of intuition to identify that a greedy algorithm is the correct algorithm. But as you’ve seen from the interval scheduling problem, you’ll notice that pure intuition may not suffice- you’re going to need some proof. It takes some creativity, not only to identify the algorithm but also to come up with a good proof. A bit of practice will do it though…
Often greedy problems are maximisation or minimisation problems. To summarise, there are 6 kinds of proofs we’ve gone through.
Formal proofs- do this to ensure you’re correct, especially when an algorithm you think should work actually doesn’t.
By exchange argument
By contradiction
By induction
Others we didn’t cover include bounding argument (showing that there is a maximum/minimum that the algorithm always achieves). Exchange argument usually suffices in these cases though.
Alternative/informal proofs- usually intuition-based and done in contest environments when time is not a luxury you can afford.
By common sense
By trial and error
Any other method that gives a correct answer, even if you don’t fully know why.
Challenge Problem
Singapore National Olympiad in Informatics
2024 Preliminary Contest
Question 5
https://codebreaker.xyz/problem/explosives
Can you find and prove the greedy algorithm? If not, refer to the solution here.
Hope you enjoyed this article! I don’t know about you, but I can prove that the greedy method to subscribe to Elucidate right now is the optimal behaviour for anyone interested in this kind of mind-stimulating content!
And if you liked it, greedily share it with whomever else you think would enjoy it. The more, the merrier- that’s the fundamental reasoning behind greedy algorithms!