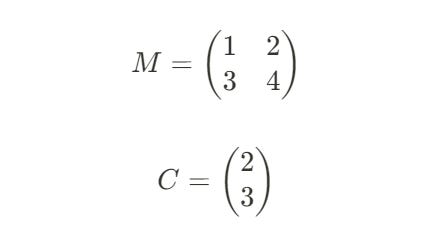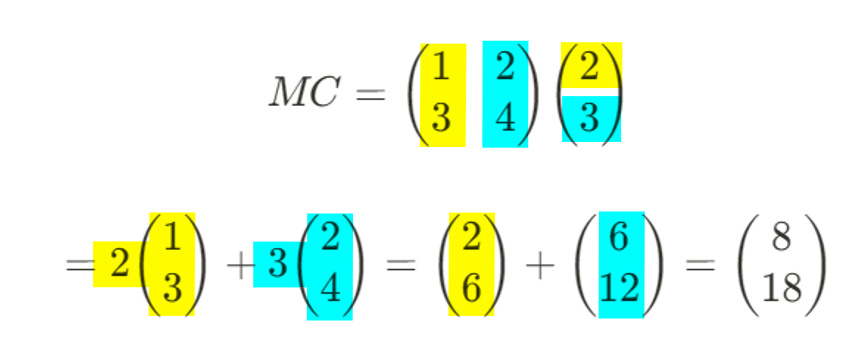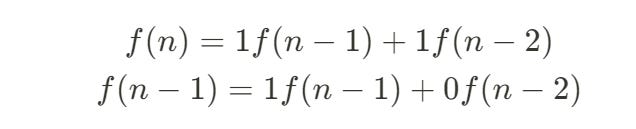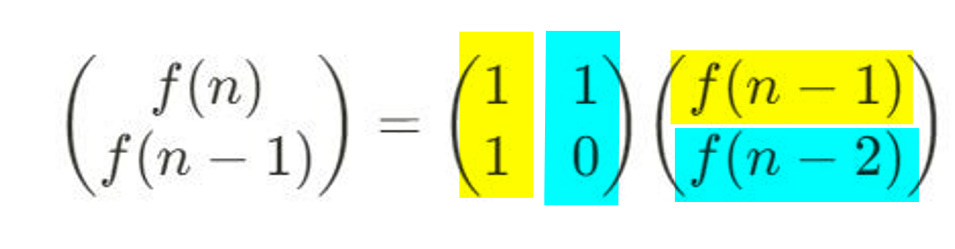You have been invited to Fibonacci city today.
For security reasons, Fibonacci city has implemented a special security protocol. In order to enter the city, every person needs a password. The citizens are numbered 1, 2, 3, and so on. The nth person’s password is the given by nth Fibonacci number. The legendary mathematician Fibonacci of Pisa himself (in spirit form, of course), rules the city that is his namesake and has given you a fun little task.
Write a program so that any citizen who enters gives their number (N) and password. If the password is the Nth Fibonacci number, then let them in. Otherwise, kick them out immediately.
What is the fastest way you can accomplish your task? Note that the city is huge. Millions live here, and thousands of people can enter the gates every second. Your program must run at lightning speed.
Fibonacci was a genius, and you can be too!
Your brain is a muscle that must be regularly exercised. Subscribe to get weekly brain workouts through interesting problems like this one.
If you’re a regular here, you can trust that I deliver quality work with every article. All I ask is less than 2 cups of coffee a month as encouragement. I trust you will make the right choice and support my crucial work.
The Fibonacci sequence
This very well known pattern follows a simple rule.
The first 2 numbers are 1 and 1. Every next number is the sum of the last 2 numbers.
The first few numbers of the pattern are,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
The naïve solution
You want to find the nth Fibonacci number, and a simple solution is to implement it directly with a function.
Let f(n) be the function that finds the nth Fibonacci number. The relation given above is,
f(1) = f(2) = 1
f(n) = f(n-1) + f(n-2)
int f(int n) {
if (n == 1 || n == 2) return 1;
if (n > 2) return f(n-1) + f(n-2);
else return -1; // invalid input
}It takes O(n) time for this function to find f(n) and this is too slow. We need a faster solution, and that’s going to need a bit of maths. And also a new data structure.
Introducing matrices
Unlocking this new data structure will take a mathematical trick called matrices. They are a very cool mathematical wonder with plenty information available about them online, but for now a quick introduction will do.
A matrix is something that has rows and columns, like a table or spreadsheet but with only numbers and no labels. Let’s create an example matrix, M, with 2 rows and 2 columns. This is a 2x2 matrix.
A column matrix has only 1 column. A row matrix has exactly one row. These are special matrices. Let’s create a row matrix, R, and a column matrix, C.
Simple? Let’s move on.
Multiplying matrices
There are 3 ways matrices are multiplied. Starting off, to multiply a matrix by a whole number, just multiply every number in the matrix by that whole number.
In general,
The second step we’ll learn is multiplying a matrix by a column matrix. To do this, there are 2 things to keep in mind
We always write this as M times C, where C is the column matrix and M is whatever matrix we want to multiply. We don’t go the other way around (C times M is invalid).
The number of rows in C must be the same as the number of columns in M
To carry out the multiplication,
Multiply all the numbers in the first column of M by the number in the first row of C
Multiply all the numbers in the second column of M by the number in the second row of C
Repeat until complete
When done, convert M into a column matrix by adding up all the numbers in each row.
Here’s an illustration. Let’s define M and C like this.
Let’s carry out the multiplication step-by-step.
Each row in C is assigned a column in M.
See what we did there? We broke up the column matrix to find the answer.
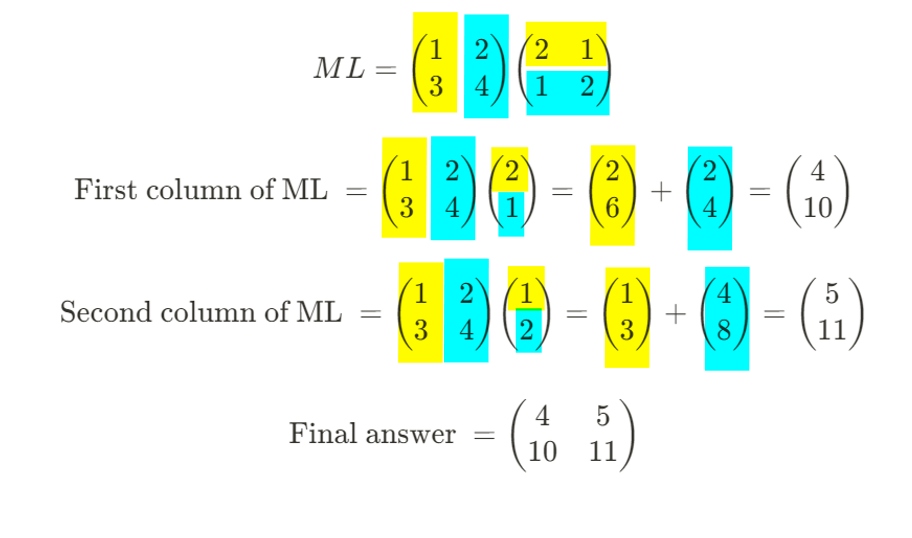
Finally, we can generalise this process because any matrix can just be broken up into multiple columns. So if we have this,
We know L has 2 columns. So we carry out the division column by column.
With that out of the way, it’s time to think about using matrices to represent the Fibonacci numbers.
The Fibonacci matrix
You first write a simple equation.
The first equation is simple, we already know it. The second equation is just a fancy way of writing f(n-1) = f(n-1) if you think about it.
But does the equation look a bit familiar?
Hmm… this alignment makes it look familiar. Have we seen this before?
Can it be that simple? It’s a matrix!
Getting a relation
Now that we have an answer, we can do some more cool maths.
We can use this to write our equation.
You can generalise this.
Great! Now, all we need is a method to rapidly calculate M^(n-2). And here’s where we have just the trick.
Fast matrix powers
At first, you feel stuck. If you calculate M^(n-2) using recursion by repeatedly multiplying M by itself n-2 times, you have an O(n) solution again. However, there is a much faster way.
You can express any number in binary. You remember that binary writes numbers as sums of powers of 2. Suppose then that we write n-2 in binary as you can express any number in binary.
Where b1, b2, etc are powers of 2.
You realise something magical- you only need to keep track of the value of M to the power of numbers that are a power of 2.
So let us create an array of matrices, and we call it memo.
memo[i] stores M^(2^i)memo[0] is just M. So we can build from there.
For any i, you can do some more maths to find a cool pattern.
Multiplying a 2-by-2 matrix by another 2-by-2 matrix is easy, and you can also generalise that if you’d like.
Since the matrix is 2x2 and this is small, we can consider the time to multiply 2 matrices as O(1). Since we are using binary, we only need to store log(N) matrices in memo. After that, all we need to do is find the binary representation of n-2. Then, multiply all memo[b] for every power 2^b that is in the binary representation of n-2 to find M^(n-2) in O(log(N)). This is significantly faster than our initial solution!
Final challenge and reflection
You discover you have taken a beautiful mathematical journey to find a new data structure- the matrix. Using the matrix and an array, you’ve discovered a fast way to find the nth Fibonacci number! Fibonacci himself approaches you to let you know how proud he is.
As a final challenge, your job is to actually code a program to find the nth Fibonacci number using your newfound skills. Also comment below, how did you like this exploration, what did you learn, and do you have any more comments? Finally, if you enjoy content like this, remember that I only ask less than 2 cups of coffee a month for your support.
Thanks for reading, and I’ll see you in the next one!
Please consider supporting my work if you enjoy these problem-solving adventures. All I ask is less than 2 cups of coffee a month.
Please comment on this article,
What did you learn?
Can you explain why we use this method an why it’s so fast?
What problem solving techniques from this problem can you use in general?
Eager to hear from you.
See you in the next one!