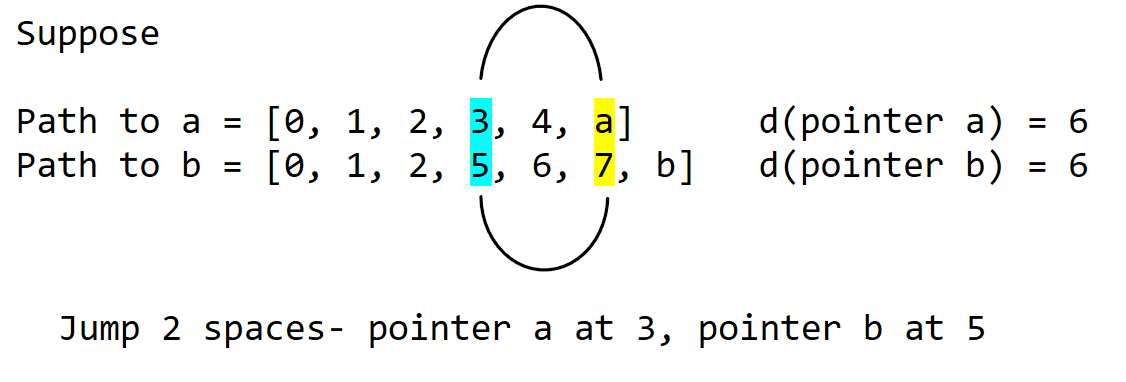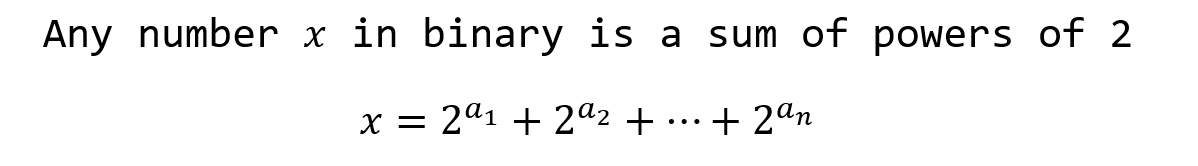Cities and roads
The lowest common ancestor problem and its solution
Another map-based problem today.
Your intelligence has become world renowned and today you are approached by a king from a land far far away. He writes a letter to you as such.
Dear curious coder,
Our country is populated by fools. It is very sad. Because the fools are not very smart, we needed to design the national rail system with very peculiar constraints.
Every city has one rail station
Some pairs of cities are directly connected by a bi-directional railway line (trains go both ways between 2 connected cities)
The connected cities are chosen such that it is possible to reach any city from any other city through some series of trains
There is exactly one way to reach any city from any other. There are no cyclic train paths.
Despite it being so simple, the fools want more. Their latest demand is,
A program that allows any fool to choose a starting and ending city, and be told exactly how much time it will take for the train to reach the destination.
You are given a railway map in the form of a list of pairs of cities that are directly connected by rail, along with the time in hours it takes the train to travel between those 2 specific cities. Using that information, please please create a program that does this for us quickly.
I will remind you, though, that there are hundreds of cities connected. This system is used by hundreds of thousands of people every second. So it better be quick. If it doesn’t work- it’s off with your head!
Good day.
~ King Bartholomew
Your head is (likely) very precious to you, so you decide to get to work immediately.
If you value your head, surely you value what’s inside it.
Your brain is a muscle that must be regularly exercised. Subscribe to get weekly brain workouts through interesting problems like this one.
If you’re a regular here, you can trust that I deliver quality work with every article. All I ask is less than 2 cups of coffee a month as encouragement. I trust you will make the right choice and support my crucial work.
The direct solution
You easily recognise that you can model this country as a graph, with cities being vertices. 2 cities (nodes) have an edge if they are directly connected by a rail. The weight of the edges represents the time taken for a train to travel between those 2 cities.
The initial solution that occurs to you is to just implement the task directly. Every time someone feeds your program a source and a destination, you run depth-first search to find the path between the starting and ending cities.
Of course, if the solution were that simple, you wouldn’t even be here. You value your head, so you decide to confirm whether or not the solution actually works.
Time to search for better solutions.
Why not just pre-compute?
You consider pre-computing the distance between all pairs of cities. After all, there are only V^2 = 10000 pairs possible right? Well, that is one working solution, but it has 2 weaknesses.
If you update the railway, you have to add a new row in O(V). Not bad, but we can do better.
It takes O(V^2) space since there are V^2 total pairs possible. Not bad, but we can do better.
Pre-computing takes O(V^2) time. Not bad, but we can do better.
To summarise, pre-computing is not bad. But we can do better. In fact, the final solution relies on pre-computing, we just have to be a bit smart about it with a special realisation.
Special observation- the graph is a tree
That is implied by this sentence in the King’s letter.
There is exactly one way to reach any city from any other. There are no cyclic train paths.
There are many equivalent definitions of a tree, and this is one of them. Why do you think so? If you can find a coherent explanation, comment it.
Since the edges are bi-directional, we can choose any node to be the root. For example, say that the country has 4 cities that look like this.
We can choose any node to be the root. It doesn’t really matter. The following 2 are equivalent ways of illustrating the city. It doesn’t matter since the nodes and edges are the same.
Why do we need a root? Because this makes dealing with the tree easier. We can find the shortest distance from any node to any other using depth-first search in O(V). But, as mentioned, we can do better. Let’s use some maths.
Elementary mathematics
Let’s choose vertex 0 to be the root of this tree.
Now imagine a function dist(a,b) that magically gives us the distance from node a to b. Let’s calculate dist(0,b) for all nodes b. This is just a single O(V) operation.
Let’s try to generalise a formula to find dist(a,b) for any a and b. For illustration, let a = 4, b = 2. Let’s assign weights to the edges and calculate the distances. What do we notice?
If we take the sum of the entire path, we see that dist(0,1) is counted twice. Why? Because the distance from 0 to 4 is the same as the distance from 0 to 1 plus the distance from 1 to 4. We can break the journey into 2 parts. Let’s write this down mathematically.
Notice that we can split up the path from a to b into the path from a to 1 and then the path from 1 to b. This is because node 1 happens to lie on the path from a to b.
Now we use the previous equations.
Since dist(0,a), dist(0,b) and dist(0,1) have all been pre-computed, we have our answer.
Generalising the equation
In this case, the common node we used was 1. But this may not be the case for all trees. In general, if we have 2 nodes a and b, we define this node as the lowest common ancestor of a and b. This is denoted by the function lca(a,b).
The lowest common ancestor lca(a,b) between the nodes a and b is defined as the last node that is common to the path from 0 to a and also 0 to b
In the above case, we found that lca(2,4) = 1. All we need now is a way to store the lowest common ancestor of any 2 nodes. And we so happen to have just the thing to help.
A naïve solution would be to manually trace out the path from 0 to a and 0 to b every single time, and find the last common node on these 2 paths. But this would be too slow, so you have to find a smarter method.
Another observation
We coin a new term (yes, there’s many new terms, but it’s an easy one I promise).
Let d(x) represent the depth of some node x. d(x) is the number of nodes on the path from 0 to x, including the nodes 0 and x themselves.
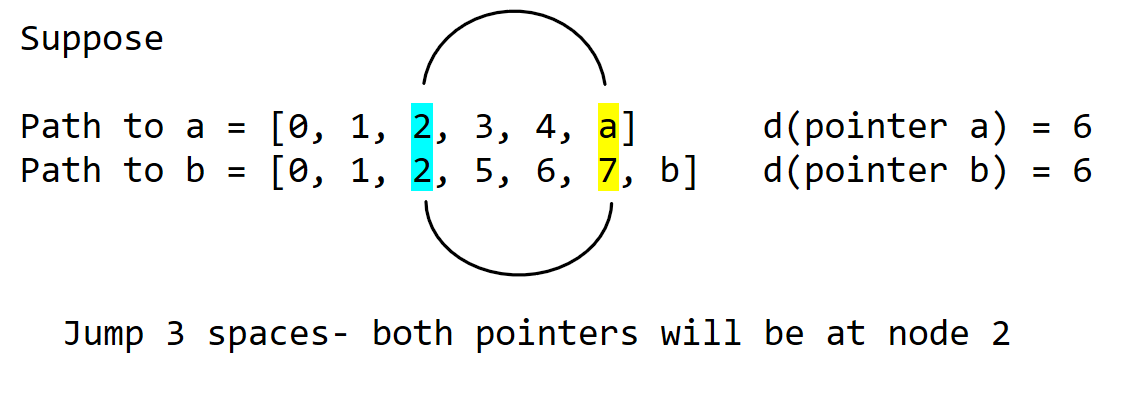
To do this, imagine 2 pointers at nodes a and b. The pointer is the yellow highlight.
We want d(pointer a) = d(pointer b). If this is not true, move the pointers till it is true.
If both walk up the path too much, we land on the same node.
If both pointers walk up the path too little, they end up at different nodes.
To find lca(a,b), we want to know,
What is the smallest number of jumps I need to so pointers a and b will end up at the same node?
If both pointers jump that number of nodes towards the root, both end up at lca(a,b)
Final answer:
Finding the lowest common ancestor
Suppose we have finished the step of ensuring d(pointer a) = d(pointer b). Now, let’s say the pointers must jump x vertices along the path from either pointer towards vertex 0 in order to reach the lca. In other words, lca(a,b) is x jumps away.
We can write x in binary.
Let’s say there are N cities. The largest jump we can take is N steps from the pointer.
So we start a counter k from log N. The logarithm is in base 2. We want to find, which powers of 2 are included in the binary representation of x?
Start with k = log(N)
Imagine moving the pointers 2^k steps closer to 0
If they will land on the same vertex, k is too big
Otherwise, k is small enough to be included
In this case, actually move the pointers 2^k steps closer to the root
Reduce k by 1
Continue the process
Once completed (k = 0), simply move either pointer up by one space. You have the answer.
Let’s try this with the previous example.
Imagine there are 10 vertices. log(10) = 3 (rounded down). So we start with k = 3. 2^3 = 8, but the pointers don’t have space to jump 8 spaces so they stop when they reach the root.
Now we set k = k-1 = 2.
Move down to k = 1.
Finally, we move the pointers and try k = 0.
The furthest we can move along the path without landing both pointers at the same node is 2 spaces. This means that if we go one more space, we land at the first common vertex, vertex 2.
Hence, lca(a,b) = 2.
Pre-computation table
This is the last step, it’s really simple. We want to speed up the “jump 2^k steps” part.
Create a table, memo
memo[k][i] is the result of jumping 2^k spaces closer to the root from vertex i
memo[k][0] = 0 for all k (you can't jump closer from the root itself)
Since the graph is a tree, we can easily track memo[0][i] for all i (1 step closer to the root). Do this using a dfs function
function dfs(node) {
for every neighbour of node {
if neighbour has not been visited {
memo[0][neighbour] = node
dfs(neighbour)
}
}
}
call dfs(0)
Now we need the following recursion formula.
for k from 1 to log N {
for i from 1 to N {
memo[k][i] = memo[k-1][memo[k-1][i]]
}
}Why does the recursion work? Jumping 2^k steps from i is the same as jumping 2^(k-1) steps twice.
Since we only need k up to log(N), this table has space O(Nlog(N)), far better than N^2. It can be initialised in O(Nlog(N)) as well.
The algorithm also only takes O(log(V)) in the worst case to find lca(a,b). After that, just use the formula.
dist(a,b) = dist(0,a) + dist(0,b) - 2*dist(0,lca(a,b))As a shorthand, we can create an array d such that,
d[i] = dist(0,i)
dist(a,b) = d[a] + d[b] - 2*d[lca(a,b)]Conclusion
You present your solution to the pleased King.
This has been a long journey. I’ll let you comment your reflections- what did you learn and did you enjoy it?
Thanks for reading, and I’ll see you in the next one!
Please consider supporting my work if you enjoy these problem-solving adventures. All I ask is less than 2 cups of coffee a month.
Please comment on this article,
What did you learn?
Can you explain why the definition of a tree given above is valid?
What problem solving techniques from this problem can you use in general?
Eager to hear from you.
See you in the next one!